Find the mean and variance for the following data
(i)Find n natural numbers.
(ii)First 10 multiple of 3.
The correct Answer is:(i)n+12,n2−112, (ii)16.5, 74.25
To solve the problem of finding the mean and variance for the given data, we will break it down into two parts as outlined in the question.
Part (i): Mean and Variance of the first n Natural Numbers
1. Identify the Data:
The first n natural numbers are: 1,2,3,…,n.
2. Calculate the Mean:
The mean ¯x is calculated using the formula:
¯x=Sum of all observationsTotal number of observations=1+2+3+…+nn
The sum of the first n natural numbers is given by the formula:
Sn=n(n+1)2
Therefore, the mean becomes:
¯x=n(n+1)2n=n+12
3. Calculate the Variance:
The variance σ2 is calculated using the formula:
σ2=∑x2in−¯x2
The sum of the squares of the first n natural numbers is given by:
∑x2i=n(n+1)(2n+1)6
Thus, the variance becomes:
σ2=n(n+1)(2n+1)6n−(n+12)2
Simplifying this gives:
σ2=(n+1)(2n+1)6−(n+1)24
Finding a common denominator (12):
σ2=2(n+1)(2n+1)−3(n+1)212
Expanding and simplifying:
σ2=(n+1)(2n+1−3(n+1))12=(n+1)(n−2)12
Part (ii): Mean and Variance of the First 10 Multiples of 3
1. Identify the Data:
The first 10 multiples of 3 are: 3,6,9,12,15,18,21,24,27,30.
2. Calculate the Mean:
The mean ¯x is calculated as:
¯x=3+6+9+12+15+18+21+24+27+3010
The sum is:
3+6+9+12+15+18+21+24+27+30=165
Therefore, the mean is:
¯x=16510=16.5
3. Calculate the Variance:
The variance σ2 is calculated using:
σ2=∑(xi−¯x)2n
First, we calculate xi−¯x for each xi:
- For 3: 3−16.5=−13.5
- For 6: 6−16.5=−10.5
- For 9: 9−16.5=−7.5
- For 12: 12−16.5=−4.5
- For 15: 15−16.5=−1.5
- For 18: 18−16.5=1.5
- For 21: 21−16.5=4.5
- For 24: 24−16.5=7.5
- For 27: 27−16.5=10.5
- For 30: 30−16.5=13.5
Now, squaring these results:
- (−13.5)2=182.25
- (−10.5)2=110.25
- (−7.5)2=56.25
- (−4.5)2=20.25
- (−1.5)2=2.25
- (1.5)2=2.25
- (4.5)2=20.25
- (7.5)2=56.25
- (10.5)2=110.25
- (13.5)2=182.25
Summing these squared values:
182.25+110.25+56.25+20.25+2.25+2.25+20.25+56.25+110.25+182.25=742.5
Finally, the variance is:
σ2=742.510=74.25
Summary of Results
- For the first n natural numbers:
- Mean: n+12
- Variance: (n+1)(n−2)12
- For the first 10 multiples of 3:
- Mean: 16.5
- Variance: 74.25
The first n natural numbers are: 1,2,3,…,n.
The mean ¯x is calculated using the formula:
¯x=Sum of all observationsTotal number of observations=1+2+3+…+nn
The sum of the first n natural numbers is given by the formula:
Sn=n(n+1)2
Therefore, the mean becomes:
¯x=n(n+1)2n=n+12
The variance σ2 is calculated using the formula:
σ2=∑x2in−¯x2
The sum of the squares of the first n natural numbers is given by:
∑x2i=n(n+1)(2n+1)6
Thus, the variance becomes:
σ2=n(n+1)(2n+1)6n−(n+12)2
Simplifying this gives:
σ2=(n+1)(2n+1)6−(n+1)24
Finding a common denominator (12):
σ2=2(n+1)(2n+1)−3(n+1)212
Expanding and simplifying:
σ2=(n+1)(2n+1−3(n+1))12=(n+1)(n−2)12
The first 10 multiples of 3 are: 3,6,9,12,15,18,21,24,27,30.
The mean ¯x is calculated as:
¯x=3+6+9+12+15+18+21+24+27+3010
The sum is:
3+6+9+12+15+18+21+24+27+30=165
Therefore, the mean is:
¯x=16510=16.5
The variance σ2 is calculated using:
σ2=∑(xi−¯x)2n
First, we calculate xi−¯x for each xi:
- For 3: 3−16.5=−13.5
- For 6: 6−16.5=−10.5
- For 9: 9−16.5=−7.5
- For 12: 12−16.5=−4.5
- For 15: 15−16.5=−1.5
- For 18: 18−16.5=1.5
- For 21: 21−16.5=4.5
- For 24: 24−16.5=7.5
- For 27: 27−16.5=10.5
- For 30: 30−16.5=13.5
- (−13.5)2=182.25
- (−10.5)2=110.25
- (−7.5)2=56.25
- (−4.5)2=20.25
- (−1.5)2=2.25
- (1.5)2=2.25
- (4.5)2=20.25
- (7.5)2=56.25
- (10.5)2=110.25
- (13.5)2=182.25
182.25+110.25+56.25+20.25+2.25+2.25+20.25+56.25+110.25+182.25=742.5
Finally, the variance is:
σ2=742.510=74.25
- For the first n natural numbers:
- Mean: n+12
- Variance: (n+1)(n−2)12
- Mean: 16.5
- Variance: 74.25
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - STATISTICSEXERCISE - Objective A(Multiple Choice Questions)14videos
STATISTICS
- BOOK - MODERN PUBLICATIONCHAPTER - STATISTICSEXERCISE - Objective B(Fill in the Blanks)6videos
STATISTICS
- BOOK - MODERN PUBLICATIONCHAPTER - STATISTICSEXERCISE - Exercise 15( c) (Short Answer Type Questions)1videos
STATISTICS
- BOOK - MODERN PUBLICATIONCHAPTER - SETS EXERCISE - CHAPTER TEST 112videos
SETS
- BOOK - MODERN PUBLICATIONCHAPTER - STRAIGHT LINES EXERCISE - Chapter test12videos
STRAIGHT LINES
Similar Questions
Find the S.D. and variance of the following data:
 View Solution
View SolutionFind the variance for the following Data:
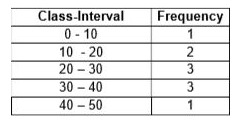 View Solution
View SolutionFind the mean and variance for each of the data :
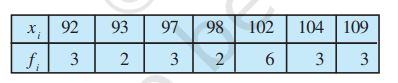 View Solution
View SolutionFind the mean and variance for each of the data :
 View Solution
View SolutionFind the mean and variance for each of the data :
First n natural numbersView SolutionFind the mean and variance for each of the data in Question:
 View Solution
View SolutionFind the mean and variance for each of the data in Question:
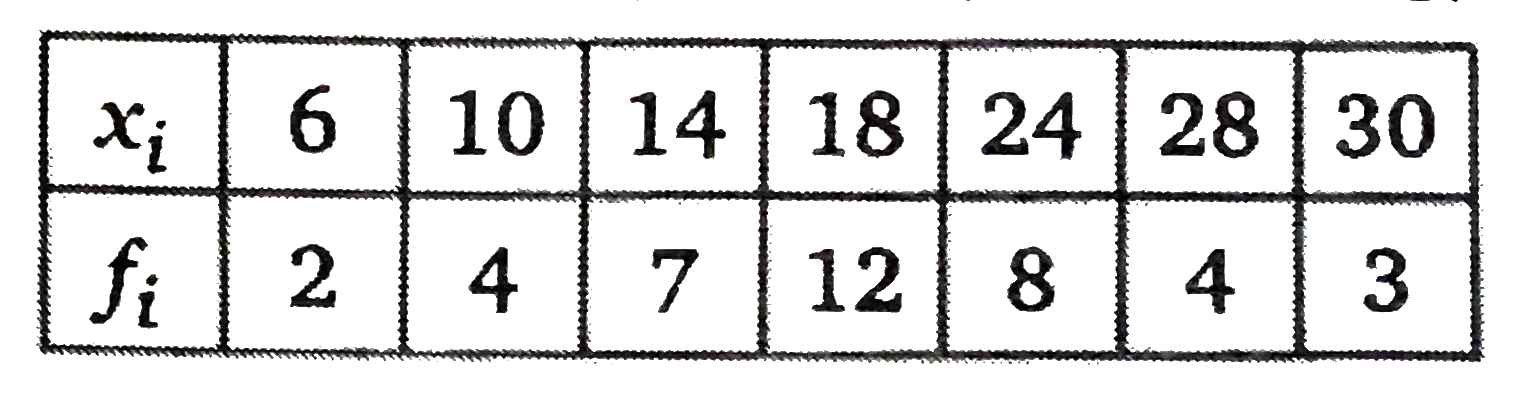 View Solution
View SolutionFind the mean and variance of first 10 multiples of 3.
View SolutionFind the sum of first n natural numbers.
View SolutionFind the variance and standard deviation for the following data:
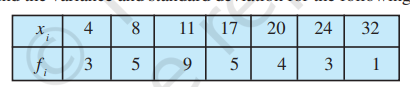 View Solution
View Solution

