Find the mean deviation from median for the following data :
36,72,46,42,60,45,53,46,51,49
The correct Answer is:B
To find the mean deviation from the median for the given data set, we will follow these steps:
Step 1: Arrange the data in ascending order
The given data is:
36, 72, 46, 42, 60, 45, 53, 46, 51, 49.
Arranging this data in ascending order, we get:
36, 42, 45, 46, 46, 49, 51, 53, 60, 72.
Step 2: Find the number of observations (n)
Count the number of observations in the data set:
n = 10 (there are 10 numbers).
Step 3: Calculate the median
Since n is even, we use the formula for the median:
Median(M)=n/2 th observation+(n/2 + 1) th observation2
Here, n/2 = 10/2 = 5, so we need the 5th and 6th observations.
From the ordered data:
- 5th observation = 46
- 6th observation = 49
Now, substituting these values into the median formula:
M=46+492=952=47.5
Step 4: Calculate the mean deviation from the median
The formula for mean deviation (MD) from the median is:
MD=∑|xi−M|n
Where xi are the data points and M is the median.
Now we will calculate |xi−M| for each observation:
- For 36: |36−47.5|=11.5
- For 42: |42−47.5|=5.5
- For 45: |45−47.5|=2.5
- For 46: |46−47.5|=1.5
- For 46: |46−47.5|=1.5
- For 49: |49−47.5|=1.5
- For 51: |51−47.5|=3.5
- For 53: |53−47.5|=5.5
- For 60: |60−47.5|=12.5
- For 72: |72−47.5|=24.5
Now, summing these absolute deviations:
∑|xi−M|=11.5+5.5+2.5+1.5+1.5+1.5+3.5+5.5+12.5+24.5=70
Step 5: Calculate the mean deviation
Now, we divide the total absolute deviation by the number of observations:
MD=7010=7
Final Answer
The mean deviation from the median is 7.
---
The given data is:
36, 72, 46, 42, 60, 45, 53, 46, 51, 49.
36, 42, 45, 46, 46, 49, 51, 53, 60, 72.
Count the number of observations in the data set:
n = 10 (there are 10 numbers).
Since n is even, we use the formula for the median:
Median(M)=n/2 th observation+(n/2 + 1) th observation2
Here, n/2 = 10/2 = 5, so we need the 5th and 6th observations.
- 5th observation = 46
- 6th observation = 49
M=46+492=952=47.5
The formula for mean deviation (MD) from the median is:
MD=∑|xi−M|n
Where xi are the data points and M is the median.
- For 36: |36−47.5|=11.5
- For 42: |42−47.5|=5.5
- For 45: |45−47.5|=2.5
- For 46: |46−47.5|=1.5
- For 46: |46−47.5|=1.5
- For 49: |49−47.5|=1.5
- For 51: |51−47.5|=3.5
- For 53: |53−47.5|=5.5
- For 60: |60−47.5|=12.5
- For 72: |72−47.5|=24.5
∑|xi−M|=11.5+5.5+2.5+1.5+1.5+1.5+3.5+5.5+12.5+24.5=70
Now, we divide the total absolute deviation by the number of observations:
MD=7010=7
The mean deviation from the median is 7.
Topper's Solved these Questions
- STATISTICSBOOK - MODERN PUBLICATIONCHAPTER - STATISTICSEXERCISE - NCERT File (Exercise 15.1)
4 Videos
- STATISTICSBOOK - MODERN PUBLICATIONCHAPTER - STATISTICSEXERCISE - NCERT File (Exercise 15.2)
3 Videos
- STATISTICSBOOK - MODERN PUBLICATIONCHAPTER - STATISTICSEXERCISE - Objective C(True/False)
3 Videos
- SETS BOOK - MODERN PUBLICATIONCHAPTER - SETS EXERCISE - CHAPTER TEST 1
12 Videos
- STRAIGHT LINES BOOK - MODERN PUBLICATIONCHAPTER - STRAIGHT LINES EXERCISE - Chapter test
12 Videos
Similar Questions
Knowledge Check
Find the mean deviation from the median of the following data
 A7.08B7C7.1D7.05
A7.08B7C7.1D7.05Find the mean deviation about median for the following data.
 A10.34B10.50C10.40D10.37
A10.34B10.50C10.40D10.37
Calculate the mean deviation from the mean for the following data:36,72,46,42,60,45,53,46,51,49
View SolutionFind the mean deviation using median for the following datas:

View SolutionFind the mean deviation about the median for the following data:
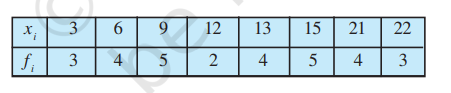
View SolutionFind the mean deviation using mean for the following datas:

View SolutionFind the mean deviation about the mean for the following data :
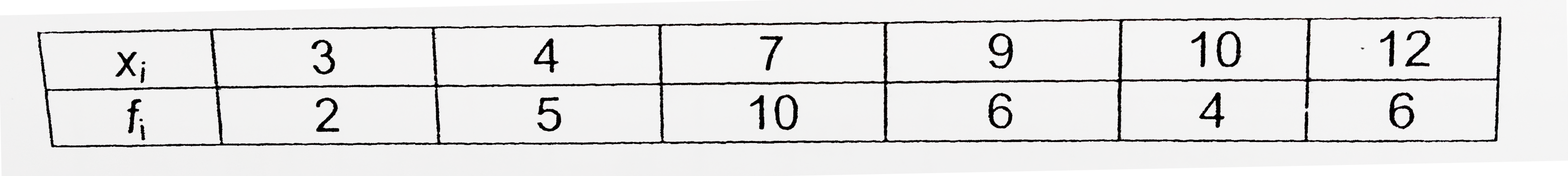
View SolutionFind the mean deviation about the mean for the following data :

View Solution


