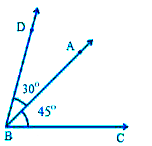
There are two set-squares in your box. What are the measures of the angles that are formed at their corners? Do they have any angle measure that is common?
To solve the question about the measures of the angles formed at the corners of the two set-squares and to find out if they have any common angle measures, we can follow these steps:
1. Identify the Angles of the First Set Square:
- The first set square has angles measuring 90 degrees, 45 degrees, and 45 degrees.
- Therefore, the angles are: 90°, 45°, 45°.
2. Identify the Angles of the Second Set Square:
- The second set square has angles measuring 90 degrees, 30 degrees, and 60 degrees.
- Therefore, the angles are: 90°, 30°, 60°.
3. List the Angles from Both Set Squares:
- From the first set square: 90°, 45°, 45°.
- From the second set square: 90°, 30°, 60°.
4. Determine Common Angles:
- Now, we will compare the angles from both set squares to find any common angles.
- The common angle between the two set squares is 90°.
5. Conclusion:
- The angles formed at the corners of the two set squares are 90°, 45°, 45° for the first set square and 90°, 30°, 60° for the second set square.
- The common angle measure between the two set squares is 90°.
Summary:
- First Set Square Angles: 90°, 45°, 45°
- Second Set Square Angles: 90°, 30°, 60°
- Common Angle: 90°
- The first set square has angles measuring 90 degrees, 45 degrees, and 45 degrees.
- Therefore, the angles are: 90°, 45°, 45°.
- The second set square has angles measuring 90 degrees, 30 degrees, and 60 degrees.
- Therefore, the angles are: 90°, 30°, 60°.
- From the first set square: 90°, 45°, 45°.
- From the second set square: 90°, 30°, 60°.
- Now, we will compare the angles from both set squares to find any common angles.
- The common angle between the two set squares is 90°.
- The angles formed at the corners of the two set squares are 90°, 45°, 45° for the first set square and 90°, 30°, 60° for the second set square.
- The common angle measure between the two set squares is 90°.
- First Set Square Angles: 90°, 45°, 45°
- Second Set Square Angles: 90°, 30°, 60°
- Common Angle: 90°
Topper's Solved these Questions
Similar Questions
Knowledge Check
An angle is twice its complementary angle what is the measure of the angle?
A30∘B90∘C60∘D120∘The measure of the angles of a triangle are in the ratio 2:7:11 . Measures of angles are
A16∘,56,88∘B18∘,63∘,99∘C20∘,70∘,90∘D25∘,175∘,105∘The ratio of the measure of an angle of a regular nonagon to the measure of its exterior angle is :
A0.12847222222222B0.20972222222222C0.29305555555556D0.17013888888889
The measure of an angle is twice the measure of its supplementary angle. Find its measure.
View SolutionDraw two acute angles and one obtuse angle without using a protractor. Estimate the measures of the angles. Measure them with the help of a protractor and see how much accurate is your estimate.
View SolutionFind the measure of an angle which forms a pair of supplementary angles with itself.
View SolutionThe ratio of the measure of an angle of a regular nonagon to the measure of its exterior angle is :
View SolutionTwo complementary angles are such that twice the measure of the one is equal to three times the measure of the other. The largest of the two measures.
View Solution