కరణాంకా సిద్దాంతం ఉపయోగించి, కింది బాహుపదులలో ప్రతి సంధర్భంలోనూ f(x) కు g(x) కరణాంకామగునో లేదో తెలపండి. f(x)=3x3+x2−20x+12,g(x)=3x−2
Step by step video & image solution for కరణాంకా సిద్దాంతం ఉపయోగించి, కింది బాహుపదులలో ప్రతి సంధర్భంలోనూ f(x) కు g(x) కరణాంకామగునో లేదో తెలపండి. f(x) =3x^(3)+x^(2)-20x+12, g(x)=3x-2 by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - బహుపదులు మరియు కరణాంకా విభజనEXERCISE - Exapmle15videos
బహుపదులు మరియు కరణాంకా విభజన
- BOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - బహుపదులు మరియు కరణాంకా విభజనEXERCISE - Exapmle15videos
బహుపదులు మరియు కరణాంకా విభజన
- BOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - నిరూపక జ్యామితిEXERCISE - Exercise87videos
నిరూపక జ్యామితి
- BOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - రెండు చరరాశులలో రేఖీయ సమీకరణాలుEXERCISE - Exercise180videos
రెండు చరరాశులలో రేఖీయ సమీకరణాలు
Similar Questions
కింద ఇవ్వబడిన బాహుపదులలో సూచించిన చరరాశి విలువను ప్రతిక్షేపించి విలువలు కనుగొనండి. X=1 వద్ద p(x)=4x2−3x+7
02:57View Solutionకింద ఇవ్వబడిన బాహుపదులలో సూచించిన చరరాశి విలువను ప్రతిక్షేపించి విలువలు కనుగొనండి. X=1 వద్ద p(x)=4x2−3x+7
01:48View Solutionఒక ఆవాస ప్రాంతంలో ప్రధాన రహదారి ఉత్తర-దక్షిణ దిశలలో ఉంది. దాని పటం కింది ఇవ్వబడినది. పటం సహాయంతో కింది ప్రశ్నలకు సమాధానాలు వ్రాయండి.
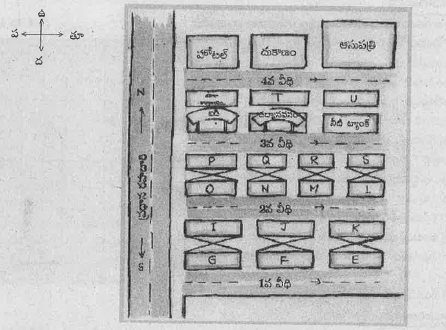 తూర్పుదిక్కున వెళ్లునప్పుడు మూడవవీధిలో ఎడమవైపు మూడోవస్థానంలో ఏం ఉంది?03:17View Solution
తూర్పుదిక్కున వెళ్లునప్పుడు మూడవవీధిలో ఎడమవైపు మూడోవస్థానంలో ఏం ఉంది?03:17View Solutionకింది రేఖాసమీకరణలను ax+by+c=0 రూపంలో రాసి, ప్రతి సందర్భంలోను a,b మరియు c విలవును రాయండి. 3x+2y=9
02:34View Solutionf'(x)>=g'(x), if f(x)=5-3x+(5)/(2)x^(2)-(x^(3))/(3),g(x)=3x-7
02:48View Solutionf(x)=3x3+x2−20x+12, g(x)=3x−2
01:54View Solutionगुणनखण्ड प्रमेय का प्रयोग कर ज्ञात कीजिए कि बहुपद g(x) बहुपद f(x) का गुणनखण्ड है अथवा नहीं।|
f(x)=3x3+x2−20x+12,g(x)=3x−201:33View SolutionIf g(x)=3x+2andg(f(x))=x, then f(2)=
11:02View SolutionIf g(x)=x3+x−2 and g(f(x))=x3+3x2+4x then f(1)+f(2) is equal to ________
14:37View SolutionIf f(x)=3x+1 and g(x)=x3+2 then (f+gf⋅g)(0) is:
View Solutionयदि f:N→I और g:I→Q इस प्रकार से परिभाषित है की f(x)=3x तथा g(x)=x+23 हो, तो gof:N→Qज्ञात कीजिए
18:02View SolutionUse the Factor Theorem to determine whether g(x) is factor of f(x) in each of the following cases :
f(x)=5x3+x2−5x−1,g(x)=x+104:28View SolutionUse the Factor Theorem to determine whether g (x) is factor of f(x) in each of the following cases:
(i) f(x)=5x3+x2−5x−1,g(x)=x+1
(ii) f(x)=x3+3x2+3x+1,g(x)=x+1
(iii) f(x)=x3−4x2+x+6,g(x)=x−2
(iv) f(x)=3x3−20x+12,g(x)=3x−2
(v) f(x)=4x3+20x2+33x+18,g(x)=2x+302:13View SolutionUse the Factor Theorem to determine whether g (x) is factor of f(x) in each of the following cases:
(i) f(x)=5x3+x2−5x−1,g(x)=x+1
(ii) f(x)=x3+3x2+3x+1,g(x)=x+1
(iii) f(x)=x3−4x2+x+6,g(x)=x−2
(iv) f(x)=3x3−20x+12,g(x)=3x−2
(v) f(x)=4x3+20x2+33x+18,g(x)=2x+304:51View SolutionUse the Factor Theorem to determine whether g (x) is factor of f(x) in each of the following cases:
(i) f(x)=5x3+x2−5x−1,g(x)=x+1
(ii) f(x)=x3+3x2+3x+1,g(x)=x+1
(iii) f(x)=x3−4x2+x+6,g(x)=x−2
(iv) f(x)=3x3+x2−20x+12,g(x)=3x−2
(v) f(x)=4x3+20x2+33x+18,g(x)=2x+301:28View Solution

