పైవాక్యములలో ప్రతిఉదాహరాల ద్వారా , అసత్యమని నిర్ణయించగల ప్రవచనములు ఏవి?x+0=x,x+1=1
Step by step video & image solution for పైవాక్యములలో ప్రతిఉదాహరాల ద్వారా , అసత్యమని నిర్ణయించగల ప్రవచనములు ఏవి?x+0=x,x+1=1 by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- గణితములో నిరూపణలుBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - గణితములో నిరూపణలుEXERCISE - Exercise
104 Videos
- ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములుBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - ఉపరితల వైశాల్యములు మరియు ఘనపరిమాణములుEXERCISE - Exercise
101 Videos
- చతుర్భుజాలుBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - చతుర్భుజాలుEXERCISE - Exercise
88 Videos
Similar Questions
కింది వాక్యములు సత్యమో లేక అసత్యమో లేక సందిగ్ధ వాక్యమో తెలియజేస్తూ వివరించండి.ఒక నెలలో 27 రోజులు కలవు.
View Solutionఈ కింద క్రమ పట్టకము యొక్కప్రక్కతల వైశాల్యము మరియు సంపూర్ణతల వైశాల్యము కనుగొనండి.
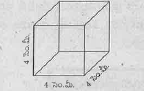
View Solutionకింది ప్రవచనాలు సత్యమో లేదా అసత్యమో తెలపండి. ప్రతి సమాంతర చతుర్భుజము ఒక ట్రెపీజియం అగును.
View SolutionLet x=1+11+11+11+ ..∞ . Which of the following is correct? x2+x+1=0 (b) x2−x+1=0 (c) x2+x−1=0 (d) x2−x−1=0
View SolutionIf f(x)=⎧⎪⎨⎪⎩−1x<00x=0andg(x)=x(1−x2), then1x>0
View SolutionFunction f ( x ) = {{:( (x + 1 ) ^( 2 -[ (1//[x] ) + 1//x])"," , x ne 0 ) , ( 0",", x = 0 ) :}
View SolutionIf f(x)={1−x, for 0<x≤112, for x=0, then in [0, 1]
View SolutionIf f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩e1x−1e1x+1, for x≠01, for x=0, then f is
View SolutionIf f(x)={11+e1/xx≠00x=0 then f(x) is
View SolutionIf ∣∣ ∣∣1+x1−x1−x1−x1+x1−x1−x1−x1+x∣∣ ∣∣=0 then x=
View SolutionIf f(x)=e1/x−1e1/x+1 for x≠0,f(0)=0 then at x=0, f(x) is
View SolutionA: f(x)=11+e1/x(x≠0)andf(0)=0 is right continuous at x=0
R: Ltx→011+e1/x=0
View SolutionA={x / -1 le x le 1}, f(x) = x^(2), g(x) = x^(3)గానిర్వచిస్తేకిందిప్రమేయాలలోఏవిసంగ్రహిస్తాయి?f : A rarr A
View SolutionA={x / -1 le x le 1}, f(x) = x^(2), g(x) = x^(3)గానిర్వచిస్తేకిందిప్రమేయాలలోఏవిసంగ్రహిస్తాయి?g : A rarr A
View SolutionThe function f(x)={e1x−1e1x+1,x≠0 0,x=0 at x=0
View SolutionShow that, f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩e1x−1e1x+1,x≠00,x=0. Is discontinuous at x= 0
View Solution