If (¯a,¯b)=30∘ then (¯a,−¯b)=
Step by step video & image solution for If (overlinea,overlineb)=30^@ then (overlinea,-overlineb)= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
If ¯a,¯b,¯c are vectors of length 4,4,5 re-spectively, and ¯a,¯b,¯c are perpendicular to ¯b+¯c,c+¯a,¯a+¯b, then ∣∣¯a+¯b+¯c∣∣=
View SolutionStatement-1: Let n≤3 and A1,A2,..,An be n independent events such that P(Ak)=1k+1 for 1≤k≤n, then
P(¯¯¯A1∩¯¯¯A2∩¯¯¯A3∩..∩¯¯¯An)=1n+1
Statement-2: Let A1,A2,A3,..,An be n(≤3) events associated to a random experiment . Then, A1,A2,..,An are independent iff P(A1∩A2∩..∩An)=P(A1)P(A2)..P(An).
View Solution
Knowledge Check
For any three vectors ¯a,¯band¯c,(¯a−¯b).[(¯b+¯c)×(¯c+¯a)] is equal to :
A¯2a.(¯bׯe)B[¯a¯b¯c]C[¯a¯b¯c]2D0Statement-1: Let n≤3 and A1,A2,..,An be n independent events such that P(Ak)=1k+1 for 1≤k≤n, then
P(¯¯¯A1∩¯¯¯A2∩¯¯¯A3∩..∩¯¯¯An)=1n+1
Statement-2: Let A1,A2,A3,..,An be n(≤3) events associated to a random experiment . Then, A1,A2,..,An are independent iff P(A1∩A2∩..∩An)=P(A1)P(A2)..P(An).AStatement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1.BStatement-1 is True, Statement-2 is True, Statement-2 is not a correct explanation for Statement-1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True.If P(A)=a,P(B)=bandP(A∩B)=c, then : P(¯¯¯A∩¯¯¯B)=
A1−a−b−cBa+b−cC1+a−b−cD1−a−b+c
If a=sin30∘andb=sin30∘, then
View SolutionIf AandB are independent events of a random experiment such that P(A∩B)=16andP(¯¯¯A∩¯¯¯B)=13 then P(A)=
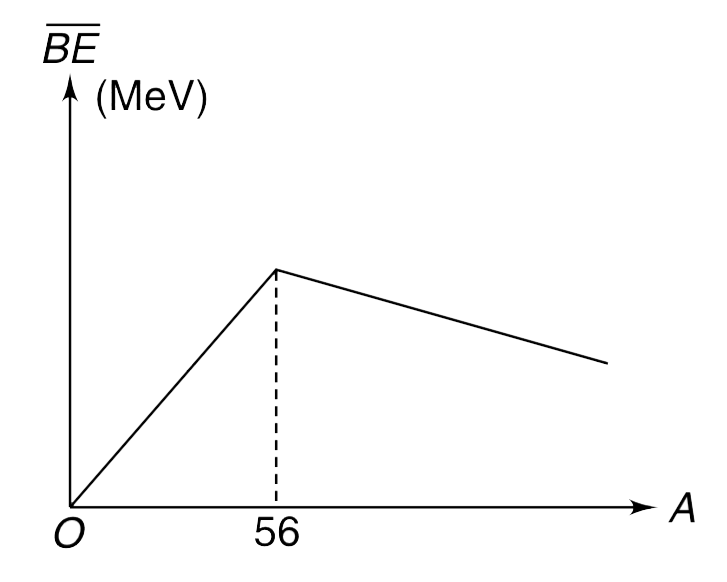
View SolutionThe graph of binding energy per nucleon (¯¯¯BE) versus mass number (A) for various nuclei has been approximated as made up of two linear components as shown in figure. The slope of line for 0<A<56 is 0.16 and slope of line for A56 is -0.012. the binding energy of .42He nucleus is 11 times the value predicted by the shown graph due to its very stable structure. Estimate the minimum mass number (A) of a nucleus for it to exhibit alpha decay.
View SolutionThe probability that at least one of the events A and B occurs is 0.6. If A and B occurs simultaneously with probability 0.2, then the value of P(¯¯¯A)+P(¯¯¯B)=1.
View SolutionIf P(¯¯¯A∪B)=56,P(A)=12andP(¯¯¯B)=23, then : P(A∪B)=
View Solution