A,B ಮತ್ತು C ಗಳು △ABC ಯ ಒಳಕೋನಗಳಾದರೆ, sin(B+C2)=cosA2ಎಂದು ತೋರಿಸಿ.
Step by step video & image solution for A,B ಮತ್ತು C ಗಳು triangle ABC ಯ ಒಳಕೋನಗಳಾದರೆ, sin (frac{B + C}{2})=cos frac{A}{2}ಎಂದು ತೋರಿಸಿ. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
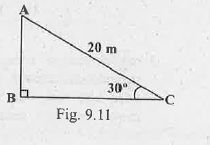
ಒಬ್ಬ ಸರ್ಕಸಿನ ಕಲಾವಿದನು, ನೇರ ಸ್ತಂಭದಿಂದ ಹಿಗ್ಗಿಸಿ ನೆಲಕ್ಕೆ ಕಟ್ಟಿರುವ 20 m ಉದ್ದದ ಹಗ್ಗದ ಮೇಲೆ ಹತ್ತುತ್ತಿದ್ದಾನೆ. ನೆಲದೊಂದಿಗೆ ಹಗ್ಗದ ನಡುವಿನ ಕೋನವು 30o ಆದರೆ, ಸ್ತಂಭದ ಎತ್ತರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ (ಚಿತ್ರ 12cdot11 ನೋಡಿ)
View Solutionಆವರಣದಲ್ಲಿ ಕೊಟ್ಟಿರುವ ಪಹ ಸೂಕ್ತವಾದ ಪದವನ್ನು ಆರಿಸಿ ಬಿಟ್ಟ ನ ದದ ತುಂಬಿಸಿ. ಬಾಹುಗಳ ಸಂಖ್ಯೆ ಒಂದೇ ಇರುವ ಎರಡು ಬಹುಭುಜಾಕೃತಿಗಳು ಸಮರೂಪವಾಗಬೇಕಾದರೆ (a) ಅದರ ಅನುರೂಪ ಕೋನಗಳು _______ಮತ್ತು (b) ಅದರ ಅನುರೂಪ ಬಾಹುಗಳು __________(ಸಮ, ಸಮಾನುಪಾತದಲ್ಲಿರುತ್ತದೆ)
View SolutionA, B and C triangle ABC If, sin (frac{B + C}{2})=cos frac{A}{2} Show that.
View SolutionAttempt the following: In △ABC, prove that tan(B−C2)=b−cb+ccot(A2)
View SolutionIn △ABC prove that sin(A2)sin(B2)sin(C2)=(A(△ABC))2abcs
View SolutionSolve the following: In △ABC prove that cos(A−B2)=a+bcsin(C2)
View SolutionIn any triangle ABC, prove that : cos frac (A+B)(2)= sin frac (C)(2) .
View SolutionIf A + B + C =pi , prove that : . sin A + sin B+sinC = 4 cos frac (A)(2) cos frac (B)(2) cos frac (C)(2) .
View SolutionIf A + B + C =pi , prove that : (sin 2A + sin 2B + sin 2C)/(cos A + cos B + cos C-1)= 8 cos frac (A)(2) cos frac (B)(2) cos frac (C)(2) .
View SolutionIf A + B + C =180^@ , prove that : cos^2 frac (A)(2)+ cos^2 frac (B)(2)+cos^2 frac (C)(2)=2+2 sin frac (A)(2)sin frac (B)(2)sin frac (C)(2) .
View SolutionIn any triangle ABC, prove that : sin frac (B-C)(2) = (b-c)/(a) cos frac (A)(2) .
View SolutionFor any triangle ABC, prove that : a+bc=cosA−B2sinC2.
View SolutionIn any triangle ABC, prove that : sinA−B2=a−bccosC2.
View SolutionIn any triangle ABC, prove that : acosB−C2=(b+c)sinA2=(b+c)cosB+C2.
View SolutionIn any triangle ABC, prove that : a−bc=sinA−B2cosC2.
View SolutionIn any triangle ABC, prove that : b−ca=sinB−C2cosA2.
View Solution
