ಕೆಳಗಿನ ಹೇಳಿಕೆಗಳನ್ನು ಪೂರ್ತಿಗೊಳಿಸಿ. ಒಂದು ಘಟನೆ E ಯ ಸಂಭವನೀಯತೆ + 'E ಅಲ್ಲದ' ಘಟನೆಯ ಸಂಭವನೀಯತೆ =________
Step by step video & image solution for ಕೆಳಗಿನ ಹೇಳಿಕೆಗಳನ್ನು ಪೂರ್ತಿಗೊಳಿಸಿ. ಒಂದು ಘಟನೆ E ಯ ಸಂಭವನೀಯತೆ + 'E ಅಲ್ಲದ' ಘಟನೆಯ ಸಂಭವನೀಯತೆ =________ by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
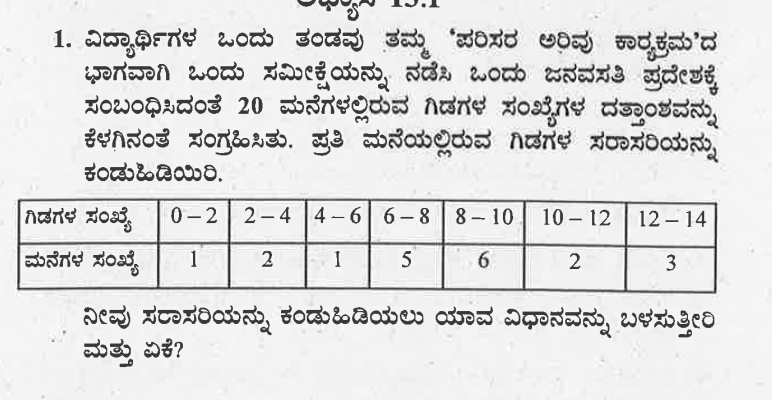
ವಿದ್ಯಾರ್ಥಿಗಳ ಒಂದು ತಂಡವು ತಮ್ಮ 'ಪರಿಸರ ಅರಿವು ಕಾರ್ಯಕ್ರಮ'ದ ಭಾಗವಾಗಿ ಒಂದು ಸಮೀಕ್ಷೆಯನ್ನು ನಡೆಸಿ ಒಂದು ಜನವಸತಿ ಪ್ರದೇಶಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ 20 ಮನೆಗಳಲ್ಲಿರುವ ಗಿಡಗಳ ಸಂಖ್ಯೆಗಳ ದತ್ತಾಂಶವನ್ನು ಕೆಳಗಿನಂತೆ ಸಂಗ್ರಹಿಸಿತು. ಪ್ರತಿ ಮನೆಯಲ್ಲಿರುವ ಗಿಡಗಳ ಸರಾಸರಿಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. ನೀವು ಸರಾಸರಿಯನ್ನು ಕಂಡುಹಿಡಿಯಲು ಯಾವ ವಿಧಾನವನ್ನು ಬಳಸುತ್ತೀರಿ ಮತ್ತು ಏಕೆ?
View Solutionಈ ಕೆಳಗಿನ ಯಾವ ಸಂದರ್ಭಗಳಲ್ಲಿ ಕೊಟ್ಟಿರುವ ಸಂಖ್ಯಾಪಟ್ಟಿಯು ಸಮಾಂತರ ಶ್ರೇಢಿಯನ್ನುಂಟು ಮಾಡುತ್ತದೆ ಮತ್ತು ಏಕೆ? ಒಂದು ಟ್ಯಾಕ್ಸಿಯ ಬಾಡಿಗೆ ಮೊದಲ ಕಿಲೋಮೀಟರ್ಗೆ Rs. 15 ಆಗಿದ್ದು ನಂತರದ ಪ್ರತಿ ಕಿಲೋಮೀಟರ್ಗೆ Rs. 8 ರಂತೆ ಇರುತ್ತದೆ.
View Solution(lim)x→∞[(e1−e)(1e−x1+x)]ξs e(1−e) (b) e(1−ee) (c) e(e1−e) (d) e(1+ee)
View Solutionif y = e ^ ((x) ^ (e ^ x)) + x ^ (e ^ (e ^ x)) + e ^ (x ^ (x ^ e)), then dy / dx = e ^ (( x) ^ (e ^ x)) x ^ (e ^ x) [e ^ xlogx + e ^ x / x] + x ^ (e ^ (e ^ x)) e ^ (e ^ x) [1 / x + e ^ xlogx] + e ^ (x ^ (x ^ e)) x ^ (x ^ e) x ^ (e-1) [1 + elogx]
View Solutionयदि e∗a=a∗e=a तब e कहलाता है -
View Solution∫e5logex−e4logexe3logex−e2logexdx का मान ज्ञात कीजिए |
View Solution∫ex−e−xe2x+e−2xdx=Alog∣∣∣ex+e−x+aex+e−x−a∣∣∣+c then (A,a)=
View SolutionThe distance between two points A and B on a highway 100 km away from one car A and the other from B B simultaneously. The cars are in one direction, ೇರೆ ಬೇರೆ ಜವದಲ್ಲಿ ಚಲಿಸಿದರೆ ಅವುಗಳಳು 5 ಗಂಟೆಗಳಲ್ಲಿ ಸಂಧಿಸುತ್ತವೆ. A ಕಾರು B ಯ ಕಡೆಗೆ, B ಕಾರು A ಯ ಕಡೆಗೆ ಚಲಿಸಿದರೆ. ಅವುಗಳು ಸಂಧಿಸಲು ಒಂದು ಗಂಟೆ ಬೇಕಾಗುತ್ತದೆ. ಹಾಗಾದರೆ ಕಾರುಗಳ ಜವಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
View SolutionThe value of ∫e5logex+e4logexe3logex+e2logexdx is
View Solution∫eeexeexdx is equal to :
View Solution(lim)x→∞[(e1−e)(1e−x1+x)]ξs e(1−e) (b) e(1−ee) (c) e(e1−e) (d) e(1+ee)
View SolutionIf y=exex+xeex+exxe , prove that dydx=exex.xex{exx+ex.logx}+xeex.eex{1x+ex.logx}+exxe.xxe.xe−1{1+elogx}
View Solutionयदि A+B+C=π,eiθ=cosθ+isinθ तथा z=∣∣ ∣ ∣∣e2iAe−iCe−iBe−iCe2iBe−iAe−iBe−iAe2iC∣∣ ∣ ∣∣ तब
View SolutionIf A+B+C=pi,e^(itheta)=costheta+isintheta And z=|(e^(2iA),e^(-iC),e^(-iB)),(e^(-iC),e^(2iB),e^(-iA)),(e^(-iB),e^(-iA),e^(2iC))| Then
View SolutionIf A+B+C=π and eiθ=cosθ+isinθ and z=∣∣ ∣ ∣∣e2iAe−iCe−iBe−iCe2iBe−iAe−iBe−iAe2iC∣∣ ∣ ∣∣, then
View Solution(lim)x→∞[(e1−e)(1e−x1+x)]ξs e(1−e) (b) e(1−ee) (c) e(e1−e) (d) e(1+ee)
View Solution
