(x1,y1) ಮತ್ತು (x2,y2) ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡದ ಮಧ್ಯ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳ ಸೂತ್ರವನ್ನು ಬರೆಯಿರಿ.
Step by step video & image solution for (x_1,y_1) ಮತ್ತು (x_2,y_2) ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡದ ಮಧ್ಯ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳ ಸೂತ್ರವನ್ನು ಬರೆಯಿರಿ. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ಕೆಳಗಿನ ಬಿಂದುಗಳ ಜೋಡಿಗಳ ನಡುವಿನ ದೂರವನು ಕಂಡುಹಿಡಿಯಿರಿ. (a,b) , (-a,-b)
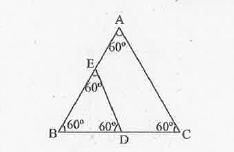
View Solution△ABC ಮತ್ತು △BDE ಗಳು ಎರಡು ಸಮಬಾಹು ತ್ರಿಭುಜಗಳು Dಯು BC ಯ ಮಧ್ಯಬಿಂದು ಆದರೆ △ABC ಮತ್ತು △BDE ಗಳ ವಿಸ್ತರಣಗಳ ಅನುಪಾತ. (A) 2 : 1 (B) 1 : 2 (C) 4 : 1 (D) 1 : 4
View SolutionThe ratio in which the line segment joining P(x1, y1) and Q(x2, y2) is divided by x-axis is y1:y2 (b) y1:y2 (c) x1:x2 (d) x1:x2
View SolutionIf the points (x1,y1),(x2,y2)and(x3,y3) be collinear, show that: y2−y3x2x3+y3−y1x3x2+y1−y2x1x2=0
View SolutionThree points A(x1,y1),B(x2,y2)andC(x,y) are collinear. Prove that: (x−x1)(y2−y1)=(x2−x1)(y−y1).
View SolutionIf the point x1+t(x2−x1),y1+t(y2−y1) divides the join of (x1,y1) and (x2,y2) internally then
View Solutionयदि तीन बिंदु (x1,y1),(x2,y2) तथा (x3,y3) संरेख है तो सिद्ध कीजिए की
(x3−x1)(y2−y1)=(x2−x1)(y3−y1)
View SolutionThe distance formula for (x_1 , y_1) and (x_2 , y_2) will be -
View SolutionIf the tangent at (x1,y1) to the curve x3+y3=a3 meets the curve again in (x2,y2), then prove that x2x1+y2y1=−1
View SolutionIf the tangents and normals at the extremities of a focal chord of a parabola intersect at (x1,y1) and (x2,y2), respectively, then (a)x1=y2 (b) x1=y1 (c)y1=y2 (d) x2=y1
View SolutionIf the tangent at (x1,y1) to the curve x3+y3=a3 meets the curve again in (x2,y2), then prove that x2x1+y2y1=−1
View SolutionThe ratio in which the line segment joining P(x1, y1) and Q(x2, y2) is divided by x-axis is (a) y1:y2 (b) y1:y2 (c) x1:x2 (d) x1:x2
View SolutionLet ¯x be the mean of x1,x2,……,xn and ¯y the mean of y1,y2……,yn ¯z is the mean of x1,x2,….,xn,y1,y2 is equal to :
View Solutionबिंदु (x1,y1),(x2,y2),(x1,y2) तथा (x2,y1) सदैव
View SolutionFind the 2×2mtrixXif[[x_1,x_2], [y_1,y_2]]-[[2,0],[0,2]]=[[3,5],[1,2]]determinex_1,x_2,y_1,y_2.
View SolutionIF [x1x2y1y2]−[2301]=[3512] then determine x1,x2,y1,y2.
View Solution
