The radius of the circle whose arc of length 15 km makes an angle of 34 radian at the centre ,is :
20cm
10cm
2222cm
1114cm
To find the radius of a circle given the length of an arc and the angle it subtends at the center, we can use the formula:
θ=ar
where:
- θ is the angle in radians,
- a is the length of the arc,
- r is the radius of the circle.
1. Identify the given values:
- Length of the arc a=15 km
- Angle θ=34 radians
2. Rearrange the formula to find the radius:
r=aθ
3. Substitute the known values into the formula:
r=15 km34
4. Simplify the division by multiplying by the reciprocal:
r=15 km×43
5. Calculate the radius:
r=15×43=15×1.3333≈20 km
Thus, the radius of the circle is 20 km.
- θ is the angle in radians,
- a is the length of the arc,
- r is the radius of the circle.
- Length of the arc a=15 km
- Angle θ=34 radians
r=aθ
r=15 km34
r=15 km×43
r=15×43=15×1.3333≈20 km
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the length of a chord of a circle is equal to that of the radius of the circle , then the angle subtended , in radians , at the centre of the circle by the chord is
A1Bπ2Cπ3Dπ4A wire of length 10cm is bent into an arc of a circle such that it subtends an angle of 1 radian at the centre. If a current of 1A is passed through the wire, the magnetic induction at the centre of the circle will be
A2×10−4 teslaB1×10−6 teslaC1×10−4 teslaD2×10−6 teslaThe radius of the circle is 14 cm, an arc is subtend an angle 54 degree at center. Find the length of the arc (in cm).
A12.8B13.2C13.8D14.2
In a circle of radius 6cm, a chord of length 10cm makes an angle of 1100 at the centre of the circle. Find: the circumference of the circle the area of the circle the length of the arc AB, the area of the sector OAB
View SolutionThe radius of a circle is 14cms. The angle subtended by an arc of the circle at the centre is 45∘. Find the length of the arc.
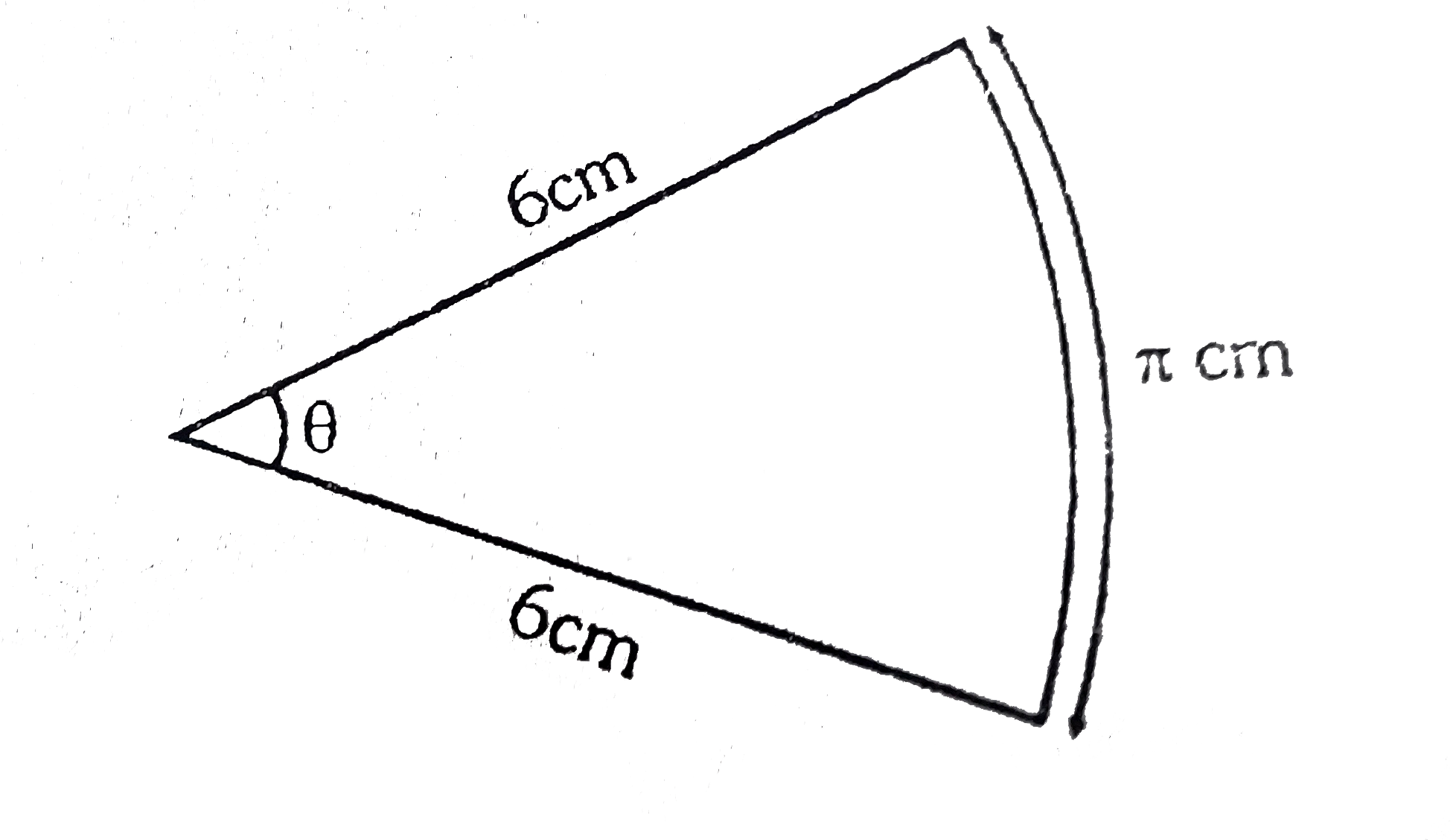
View SolutionA circular arc of length π cm. Find angle subtended by it at the centre in radian and degree.
View SolutionThe arcs of two circles whose radii are in the ratio of 4:3 subtend an angle of 48∘ each at their centres. Compare the areas of the two sectors
View SolutionA circular arc of wire of radius of curvature r subtends an angle of p/4 radian at its centre. If i current is flowing in it then the magnetic induction at its centre is -
View Solution
