The number of roots of the equation
$1 + \log_{2} (1 - x) = 2^{- x}$ , is

A

0

B

1

C

2

D

3

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

We observe that the curves $y = \log_{2} (1 - x)$ and $y = 2^{- x} - 1$ intersect at (0,0) and (-1,1) as shown in the following figure. So, the equation $1 + \log_{2} (1 - x) = 2^{- x}$ has two solutions

|

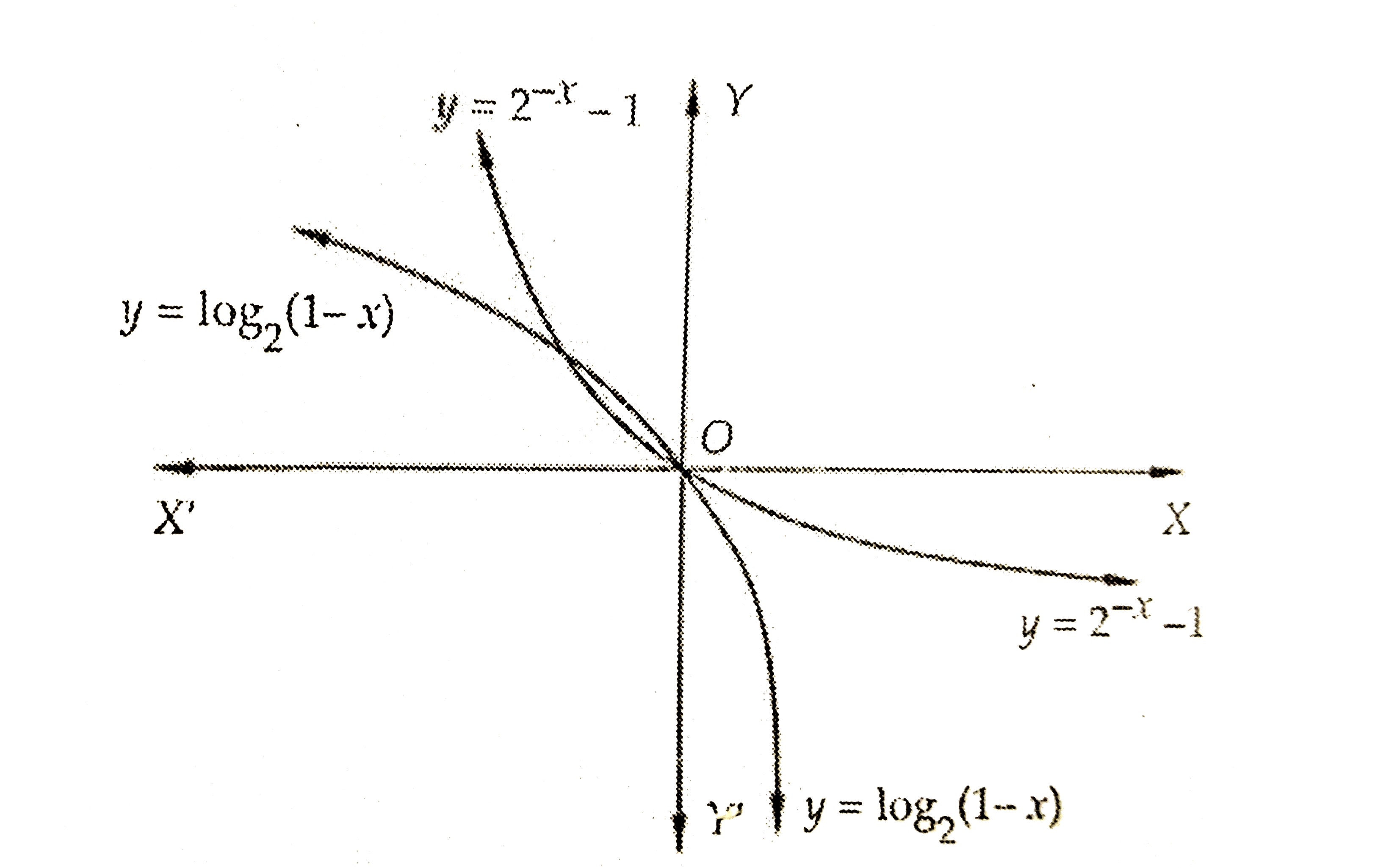
Updated on:21/07/2023

Class 12 MATHS MISCELLANEOUS EQUATIONS AND INEQUATIONS

Topper's Solved these Questions

BOOK - OBJECTIVE RD SHARMACHAPTER - MISCELLANEOUS EQUATIONS AND INEQUATIONS EXERCISE - Exercise
30videos
MISCELLANEOUS EQUATIONS AND INEQUATIONS
BOOK - OBJECTIVE RD SHARMACHAPTER - MISCELLANEOUS EQUATIONS AND INEQUATIONS EXERCISE - Chapter Test
30videos
MISCELLANEOUS EQUATIONS AND INEQUATIONS
BOOK - OBJECTIVE RD SHARMACHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test
21videos
MEASURES OF CENTRAL TENDENCY
BOOK - OBJECTIVE RD SHARMACHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31videos
PLANE AND STRAIGHT LINE IN SPACE

Similar Questions

Knowledge Check

Question 1 - Select One
The sum of the roots of the equation $x + 1 - 2 {log}_{2} (2^{x} + 3) + 2 {log}_{4} (10 - 2^{- x}) = 0$ is
A ${log}_{2} 11$
B ${log}_{2} 12$
C ${log}_{2} 13$
D ${log}_{2} 14$
Question 2 - Select One
The number of real solutions of the equation $log (- x) = 2 log (x + 1)$ is
A1
B2
C0
DNone of these
Question 3 - Select One
The number of real roots of the equation $1 + 3^{x / 2} = 2^{x}$ , is
A0
B1
C2
DNone then 2

OBJECTIVE RD SHARMA-MISCELLANEOUS EQUATIONS AND INEQUATIONS -Chapter Test

Home
Ask Doubt
Profile