Find the remainder when 101+102+103+104+105+……..+1099 is divided by 6.
The correct Answer is:zero.
To find the remainder when 101+102+103+…+1099 is divided by 6, we can follow these steps:
Step 1: Find the remainder of 10n when divided by 6
First, we will calculate the remainder of 10n for various values of n when divided by 6.
- For n=1:
101=10⇒10÷6=1(remainder 4)
- For n=2:
102=100⇒100÷6=16(remainder 4)
- For n=3:
103=1000⇒1000÷6=166(remainder 4)
From these calculations, we observe that the remainder of 10n when divided by 6 is consistently 4 for n=1,2,3.
Step 2: Generalize the result
Since 10≡4mod6, we can conclude that:
10n≡4mod6for all n≥1
Step 3: Sum the series
Now, we need to sum the series:
101+102+103+…+1099
Since each term 10n contributes a remainder of 4, we can write:
Total remainder=4+4+4+…+4(99 times)
This can be expressed as:
Total remainder=4×99=396
Step 4: Find the remainder of the total sum when divided by 6
Now, we need to find the remainder of 396 when divided by 6:
396÷6=66(remainder 0)
Conclusion
Thus, the remainder when 101+102+103+…+1099 is divided by 6 is:
0
First, we will calculate the remainder of 10n for various values of n when divided by 6.
101=10⇒10÷6=1(remainder 4)
- For n=2:
102=100⇒100÷6=16(remainder 4)
103=1000⇒1000÷6=166(remainder 4)
Since 10≡4mod6, we can conclude that:
10n≡4mod6for all n≥1
Now, we need to sum the series:
101+102+103+…+1099
Since each term 10n contributes a remainder of 4, we can write:
Total remainder=4+4+4+…+4(99 times)
This can be expressed as:
Total remainder=4×99=396
Now, we need to find the remainder of 396 when divided by 6:
396÷6=66(remainder 0)
Thus, the remainder when 101+102+103+…+1099 is divided by 6 is:
0
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - INTRODUCTORY EXERCISE - 1.134videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - INTRODUCTORY EXERCISE - 1.216videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - FUNCTIONS AND GRAPHEXERCISE - Final Round40videos
FUNCTIONS AND GRAPH
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)52videos
GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
1010+10100+101000+−−−−−+10100000000007 find R.
A0B2C4D6 - Question 2 - Select One
The remainder when 7128 is divided by 10 is
A1B3C7D9 - Question 3 - Select One
The remainder when
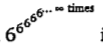 is divided by 10 is :A3B6C0Dcan't be determined
is divided by 10 is :A3B6C0Dcan't be determined
What is the remainder, when (4x4+10x3−20x2+90) is divide by ( x + 2) ?
View SolutionThe remainder when 2710+751 is divided by 10
View SolutionWhen 101+102+103+........+1099+10100 is divided by 6, the remainder obtained is
View SolutionWhen number 101+102+103+104+.............+1011 is divided by 6, the remain- der will be?
View SolutionWhen 101+102+103+.......+1032 is divided by 6, the remainder obtained is ?
View Solution

