Two pencils are the 24 cm and 42 cm . If we want to make them of equal size then minimum no. of similar pencils is :
6
11
12
None of these
The correct Answer is:B
To solve the problem of making two pencils of lengths 24 cm and 42 cm into equal sizes with the minimum number of similar pencils, we can follow these steps:
Step 1: Find the Greatest Common Divisor (GCD)
To find the minimum size of the similar pencils, we first need to determine the greatest common divisor (GCD) of the two lengths (24 cm and 42 cm).
- Calculation of GCD:
- The factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24
- The factors of 42 are: 1, 2, 3, 6, 7, 14, 21, 42
- The common factors are: 1, 2, 3, 6
- The greatest common factor is 6.
Step 2: Divide Each Length by the GCD
Next, we divide each pencil length by the GCD to find out how many similar pencils of that size can be made.
- For the 24 cm pencil:
Number of similar pencils=246=4
- For the 42 cm pencil:
Number of similar pencils=426=7
Step 3: Calculate the Total Number of Similar Pencils
Now, we add the number of similar pencils from both lengths to find the total number of similar pencils needed.
Total similar pencils=4+7=11
Final Answer
Thus, the minimum number of similar pencils of equal size is 11.
---
To find the minimum size of the similar pencils, we first need to determine the greatest common divisor (GCD) of the two lengths (24 cm and 42 cm).
- The factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24
- The factors of 42 are: 1, 2, 3, 6, 7, 14, 21, 42
- The common factors are: 1, 2, 3, 6
- The greatest common factor is 6.
Next, we divide each pencil length by the GCD to find out how many similar pencils of that size can be made.
Number of similar pencils=246=4
Number of similar pencils=426=7
Now, we add the number of similar pencils from both lengths to find the total number of similar pencils needed.
Thus, the minimum number of similar pencils of equal size is 11.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - INTRODUCTORY EXERCISE - 1.59videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - INTRODUCTORY EXERCISE - 1.65videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - INTRODUCTORY EXERCISE - 1.33videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - FUNCTIONS AND GRAPHEXERCISE - Final Round40videos
FUNCTIONS AND GRAPH
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)52videos
GEOMETRY
Similar Questions
Question #2 Sumit went to the market with Rs. 100. If he buys three pens and six pencils he uses up all his money. On the other hand, if he buys three pencils and six pens he would fall short by 20%. If he wants to buy equal number of pens and pencils, how many pencils can he buy?
View SolutionA tailor used 25 m 75 cm of cloth to make 5 trousers of equal size. What length of cloth did he use to make each?
View Solution
Knowledge Check
- Question 1 - Select One
Miss Sumitha has three drumsticks in her kitchen which are 72 cm ,90 cm and 84 cm, respectively. She wanted to cut them into equal size of pieces. Find the minimum number of pieces that she can cut.
A41B58C48D54 - Question 2 - Select One
The perimeter of two squares are 24 cm and 32 cm. The perimeter (in cm) of a third square equal in area to the sum of the areas of these squares is :
A45B40C32D48 - Question 3 - Select One
The perimeter of two squares are 24 cm and 32 cm. The perimeter (In cm) of a third square equal in area to the sum of the areas of these squares is :
A45B40C32D48
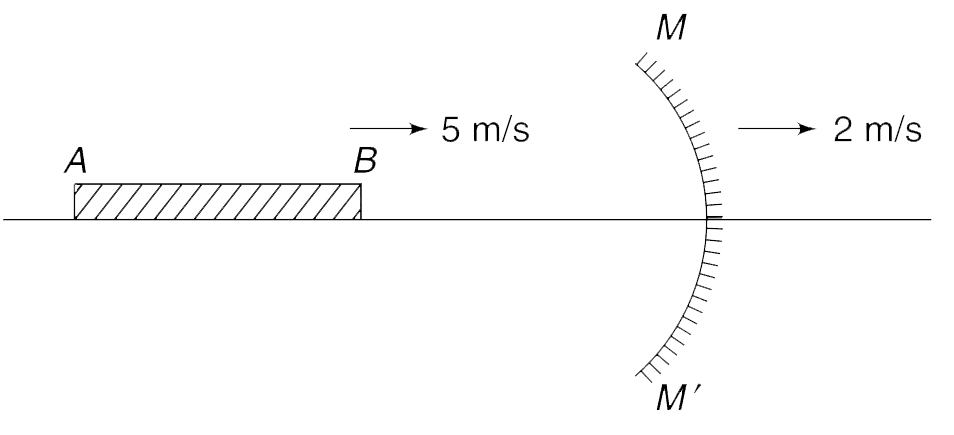
A pencil (AB) of length 20 cm is moving along the principal axis of a concave mirror MM', with a velocity 5m/s approaching the mirror. The mirror itself is moving away from the pencil at a speed of 2 m/s. Find the rate of change of length of the image of the pencil at the instant end A is at a distance of 60 cm from the mirror.
 View Solution
View SolutionA lead pencil is in the shape of a cylinder. The pencil is 21 cm long with radius 0.4 cm and its lead is of radius 0.1 cm. What is the volume of wood in the pencil ?
View SolutionThe perimeter of two squares is 24 cm and 32 cm. The perimeter (in cm) of a third square equal in area to the sum of the areas of these squares is:
View SolutionThe parallel sides of a trapezium are 24 cm and 20 cm. The distance between them is 7 cm. Find the radius of a circle whose are is equal to the area of the trapezium.
View SolutionTo measure the length of a pencil by a broken scale, one puts the pencil like this.

One end of the pencil reads 4 cm. The other end reads 13.8 cm. The length of the pencil isView Solution

