When we divide 15192327 by 99 the remainder will be :
98
84
30
None of these
The correct Answer is:B
To find the remainder when dividing 15192327 by 99, we can follow these steps:
Step 1: Perform the Division
We will divide 15192327 by 99.
15192327÷99≈153,000
Step 2: Multiply the Quotient by Divisor
Now, we multiply the quotient 153,000 by 99 to find the largest multiple of 99 that is less than or equal to 15192327.
153000×99=15147000
Step 3: Subtract to Find the Remainder
Next, we subtract this product from 15192327 to find the remainder.
15192327−15147000=45327
Step 4: Divide Again to Find the Final Remainder
Now, we need to divide 45327 by 99 to find the final remainder.
45327÷99≈458
Step 5: Multiply Again
Multiply 458 by 99:
458×99=45342
Step 6: Subtract Again
Now, subtract this from 45327:
45327−45342=−15
Since we cannot have a negative remainder, we adjust this by adding 99:
−15+99=84
Conclusion
Thus, the remainder when 15192327 is divided by 99 is 84.
Final Answer
The remainder is 84.
---
We will divide 15192327 by 99.
Now, we multiply the quotient 153,000 by 99 to find the largest multiple of 99 that is less than or equal to 15192327.
Next, we subtract this product from 15192327 to find the remainder.
Now, we need to divide 45327 by 99 to find the final remainder.
Multiply 458 by 99:
Now, subtract this from 45327:
Thus, the remainder when 15192327 is divided by 99 is 84.
The remainder is 84.
Topper's Solved these Questions
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - LEVEL 2
123 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - FINAL ROUND
116 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - EXERCISE - MISCELLANEOUS
140 Videos
- FUNCTIONS AND GRAPHBOOK - ARIHANT SSCCHAPTER - FUNCTIONS AND GRAPHEXERCISE - Final Round
40 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)
52 Videos
Similar Questions
Knowledge Check
When
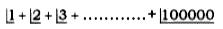 is divided by 8 then the remainder will be? A2B3C1D4
is divided by 8 then the remainder will be? A2B3C1D4When
 is divided by 12 then the remainder will be? A9B8C7D6
is divided by 12 then the remainder will be? A9B8C7D6A number when divided by 5 leaves a remainder of 4, when the double (i.e., twice) of that number is divided by 5 the remainder will be :
A0B1C3Dcan't be determined
A positive integer when divided by 425 gives a remainder 45. When the same number is divided by 17, the remainder will be
View SolutionWhen 121012 is divided by 12, the remainder is
View SolutionWhen 121012 is divided by 12, the remainder is
View SolutionWhen
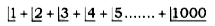 is divided by 10, the remaindeer obtained is ?
is divided by 10, the remaindeer obtained is ?
View SolutionWhen
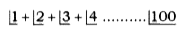 , is divided by 5, the remainder obtained is ?
, is divided by 5, the remainder obtained is ?
View Solution
