When (1!)1!+(2!)2!+(3!)3!+……+(100!)100! is divided by 5, the remainder obtained is :
2
0
4
none of these
The correct Answer is:A
To solve the problem of finding the remainder when (1!)(1!)+(2!)(2!)+(3!)(3!)+…+(100!)(100!) is divided by 5, we can break it down step by step.
Step 1: Calculate the factorials and their powers
1. Calculate (1!)(1!):
1!=1⇒(1!)(1!)=11=1
2. Calculate (2!)(2!):
2!=2⇒(2!)(2!)=22=4
3. Calculate (3!)(3!):
3!=6⇒(3!)(3!)=66
4. Calculate (4!)(4!):
4!=24⇒(4!)(4!)=2424
5. Calculate (5!)(5!):
5!=120⇒(5!)(5!)=120120
Step 2: Analyze the powers modulo 5
Next, we need to find the value of each term modulo 5.
1. For (1!)(1!)mod5:
1mod5=1
2. For (2!)(2!)mod5:
4mod5=4
3. For (3!)(3!)mod5:
- Calculate 66mod5:
6mod5=1⇒66mod5=16=1
4. For (4!)(4!)mod5:
- Calculate 2424mod5:
24mod5=4⇒424mod5
- Since 4≡−1mod5:
(−1)24mod5=1
5. For (5!)(5!)mod5:
- Since 120≡0mod5:
120120mod5=0
Step 3: Combine the results
Now we can combine the results of all the terms calculated modulo 5:
(1)+(4)+(1)+(1)+(0)+…+(0)(for terms from 6! to 100!)
The terms from 6! to 100! will all contribute 0 because they will all be multiples of 5.
So, we only need to sum the non-zero contributions:
1+4+1+1=7
Step 4: Find the remainder when divided by 5
Finally, we find the remainder when 7 is divided by 5:
7mod5=2
Final Answer
The remainder obtained when (1!)(1!)+(2!)(2!)+(3!)(3!)+…+(100!)(100!) is divided by 5 is 2.
---
1!=1⇒(1!)(1!)=11=1
2!=2⇒(2!)(2!)=22=4
3!=6⇒(3!)(3!)=66
4!=24⇒(4!)(4!)=2424
5!=120⇒(5!)(5!)=120120
1mod5=1
4mod5=4
- Calculate 66mod5:
6mod5=1⇒66mod5=16=1
- Calculate 2424mod5:
24mod5=4⇒424mod5
- Since 4≡−1mod5:
(−1)24mod5=1
- Since 120≡0mod5:
120120mod5=0
(1)+(4)+(1)+(1)+(0)+…+(0)(for terms from 6! to 100!)
1+4+1+1=7
7mod5=2
The remainder obtained when (1!)(1!)+(2!)(2!)+(3!)(3!)+…+(100!)(100!) is divided by 5 is 2.
Topper's Solved these Questions
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - FINAL ROUND
116 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 1
40 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - LEVEL 1
140 Videos
- FUNCTIONS AND GRAPHBOOK - ARIHANT SSCCHAPTER - FUNCTIONS AND GRAPHEXERCISE - Final Round
40 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)
52 Videos
Similar Questions
Knowledge Check
When
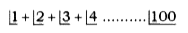 , is divided by 5, the remainder obtained is ?A0B1C2D3
, is divided by 5, the remainder obtained is ?A0B1C2D3When 221 is divided by 9, the remainder obtained is ?
Aa) 1Bb) 2Cc) 8Dd) 6When 355 is divided by 82, the remainder obtained is ?
A27B55C65D17
The remainder when (1!)2+(2!)2+(3!)2+…..+(100!)2 is divided by 144 is ab then ab=
View SolutionIf (1!)2+(2!)2+(3!)2+……..+(99!)2 is divided by 100, the remainder is
View SolutionWhen 101+102+103+........+1099+10100 is divided by 6, the remainder obtained is
View SolutionWhen 101+102+103+.......+1032 is divided by 6, the remainder obtained is ?
View SolutionIf x100−1 is divided by x2−1, then remainder will be
View Solution
