An equilateral triangle is cut from its three vertices to form a regular hexagon . What is the percentage of area wasted ?
A)20%
B)50%
C)33.33%
D)66.66%
The correct Answer is:C
To solve the problem of finding the percentage of area wasted when an equilateral triangle is cut from its three vertices to form a regular hexagon, we can follow these steps:
Step 1: Understand the Geometry
We start with an equilateral triangle and cut off its three vertices to form a regular hexagon. Let's denote the side length of the equilateral triangle as A.
Step 2: Calculate the Area of the Equilateral Triangle
The formula for the area AT of an equilateral triangle with side length A is given by:
AT=√34A2
For our example, let’s assume A=3 cm. Thus, the area of the triangle becomes:
AT=√34×32=√34×9=9√34 cm2
Step 3: Determine the Side Length of the Hexagon
When we cut the vertices of the triangle, we create a regular hexagon. Each side of the hexagon corresponds to the segments created by cutting the triangle. Since the triangle is equilateral, each side of the hexagon will be 1 cm (since the original side of the triangle is divided into three equal parts).
Step 4: Calculate the Area of the Regular Hexagon
The formula for the area AH of a regular hexagon with side length s is given by:
AH=3√32s2
Substituting s=1 cm:
AH=3√32×12=3√32 cm2
Step 5: Calculate the Area Wasted
The area wasted AW is the difference between the area of the triangle and the area of the hexagon:
AW=AT−AH
Substituting the areas calculated:
AW=9√34−3√32
To subtract these, we need a common denominator:
AH=3√32=6√34
Thus,
AW=9√34−6√34=3√34 cm2
Step 6: Calculate the Percentage of Area Wasted
To find the percentage of area wasted, we use the formula:
Percentage Wasted=(AWAT)×100
Substituting the areas:
Percentage Wasted=⎛⎜⎝3√349√34⎞⎟⎠×100=(39)×100=13×100=33.33%
Final Answer
The percentage of area wasted is 33.33%.
---
We start with an equilateral triangle and cut off its three vertices to form a regular hexagon. Let's denote the side length of the equilateral triangle as A.
The formula for the area AT of an equilateral triangle with side length A is given by:
AT=√34A2
For our example, let’s assume A=3 cm. Thus, the area of the triangle becomes:
AT=√34×32=√34×9=9√34 cm2
When we cut the vertices of the triangle, we create a regular hexagon. Each side of the hexagon corresponds to the segments created by cutting the triangle. Since the triangle is equilateral, each side of the hexagon will be 1 cm (since the original side of the triangle is divided into three equal parts).
The formula for the area AH of a regular hexagon with side length s is given by:
AH=3√32s2
Substituting s=1 cm:
AH=3√32×12=3√32 cm2
The area wasted AW is the difference between the area of the triangle and the area of the hexagon:
AW=AT−AH
Substituting the areas calculated:
AW=9√34−3√32
To subtract these, we need a common denominator:
AH=3√32=6√34
Thus,
AW=9√34−6√34=3√34 cm2
To find the percentage of area wasted, we use the formula:
Percentage Wasted=(AWAT)×100
Substituting the areas:
Percentage Wasted=⎛⎜⎝3√349√34⎞⎟⎠×100=(39)×100=13×100=33.33%
The percentage of area wasted is 33.33%.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - EXERCISE (LEVEL 2)68videos
MENSURATION
- BOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - TEST OF YOUR LEARNING18videos
MENSURATION
- BOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - EXERCISE (MISCELLANEOUS)59videos
MENSURATION
- BOOK - ARIHANT SSCCHAPTER - LOGARITHM EXERCISE - EXERCISE LEVEL 219videos
LOGARITHM
- BOOK - ARIHANT SSCCHAPTER - MIXED GRAPHEXERCISE - Higher Skill Level Questions15videos
MIXED GRAPH
Similar Questions
Knowledge Check
- Question 1 - Select One
An equilateral triangle is cut from its three vertices to form a regular hexagon . What is the percentage of area wasted ?
A20%B50%C33.33%D66.66% - Question 2 - Select One
An equilateral triangle of side 6 cm has its corners cut off to form a regular hexagon. Area (in cm2) of this regular hexagon will be
A3√3B3√6C6√3D5√32 - Question 3 - Select One
An equilateral triangle of side 6 cm has its corners cut off to form a regular hexagon. Area (in cm2) of this regular hexagon will be
A3√3B3√6C6√3D5√32
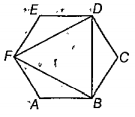
ABCDEF is a regular hexagon of side 12 cm. What is the area of traingle BDF?
 View Solution
View SolutionThe height of an equilateral triangle is 18 cm. Its area is ?
View SolutionThe height of an equilateral triangle is 6 cm. Its area is
View SolutionThe height of an equilateral triangle is 10 cm. Its area is
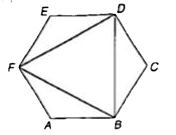
View SolutionABCDEF is a regular hexagon of side 6 cm. What is the area of triangle BDF ?
 View Solution
View Solution

