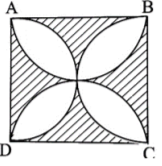
In the adjoining figure ABCD is a square . Four equal semicircles are drawn in such a way that they meet each other at 'O' . Sides AB,BC, CD and AD are the respective diameters of the four semicircles. Each of the side of the square is 8 cm. Find the area of the shaded region :

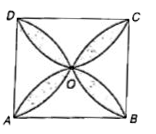
$32 (π - 2) c m^{2}$

$16 (π - 2) c m^{2}$

$(2 π - 8) c m^{2}$

$(\frac{3}{4} π - 4) c m^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Answer

Step by step video, text & image solution for In the adjoining figure ABCD is a square . Four equal semicircles are drawn in such a way that they meet each other at 'O' . Sides AB,BC, CD and AD are the respective diameters of the four semicircles. Each of the side of the square is 8 cm. Find the area of the shaded region : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.

Updated on:21/07/2023

Class 14 MATHS MENSURATION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Find the area of shaded portion if each side of the square is 14 cm.

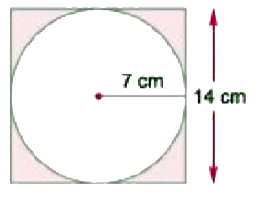A50 sq cm
B45 sq cm
C62 sq cm
D42 sq cm
Question 2 - Select One
In the adjoining figure, ABCD is a square of side 7 cm and two semicircles are drawn inside of it with AB and CD as diameters. Find the area of the shaded region (in $c m^{2}$ ).

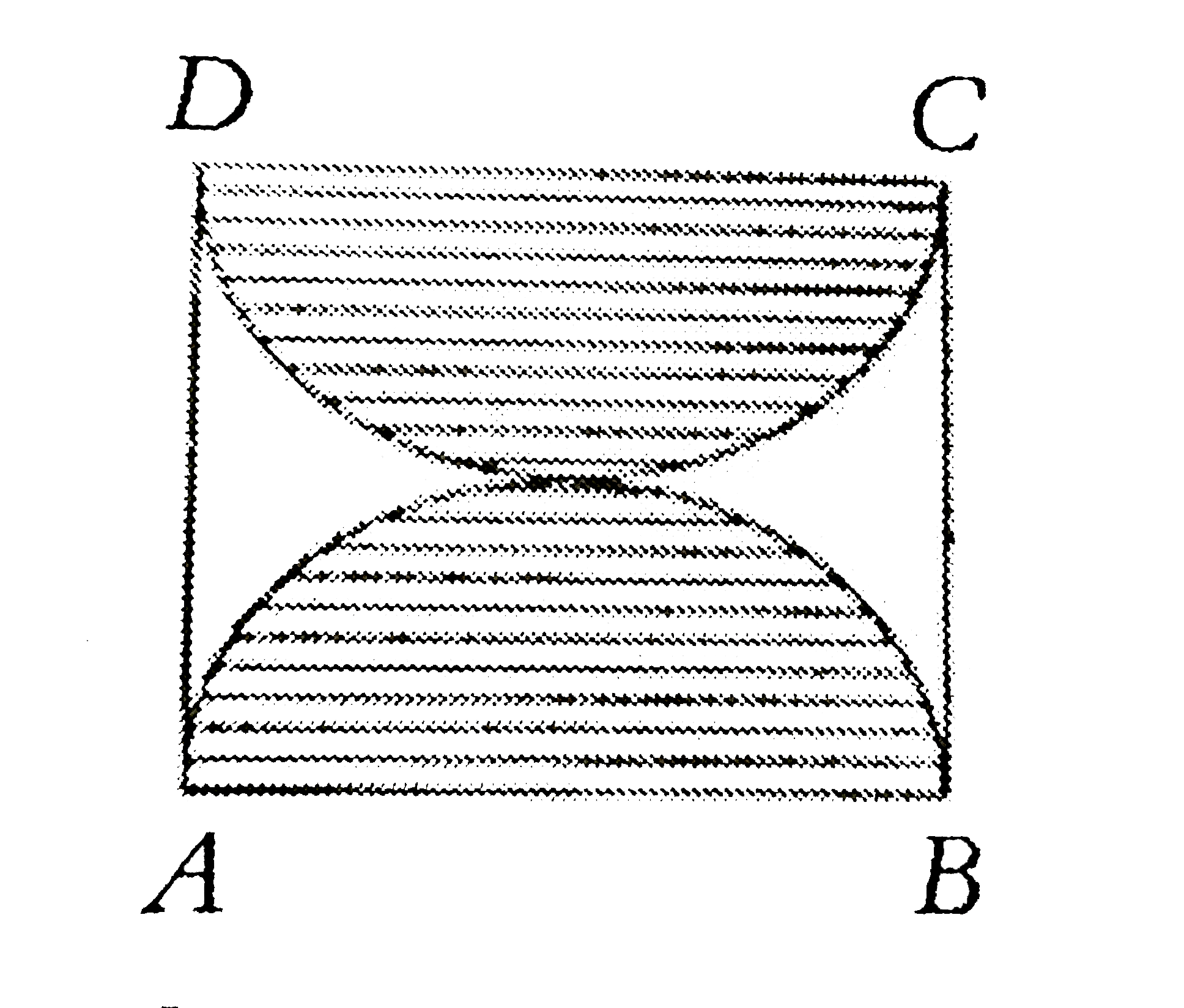A ${144 m}^{2}$
B ${164 m}^{2}$
C ${184 m}^{2}$
D ${154 m}^{2}$
Question 3 - Select One
In the adjoining figure ABCD is a square . A circle ABCD is passing through all the four vertices of the square. There are two more circles on the sides AD and BC touching each other inside the square , AD and BC are the respective diameters of the two smaller circles. Area of the square is $16 c m^{2}$ .

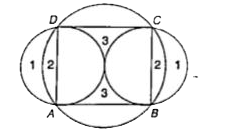
What is the area of region 2 ?
A $3 (π - 2) c m^{2}$
B $(π - 3) c m^{2}$
C $(2 π - 3) c m^{2}$
D $4 (π - 2) c m^{2}$