A regular hexagon is inscirbed in a circle of radius R . Another circle is inscribed in the hexagon . Now another hexagon is inscribed in the second ( smaller ) circle .
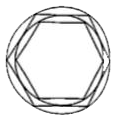
A regular hexagon is inscirbed in a circle of radius R . Another circle is inscribed in the hexagon . Now another hexagon is inscribed in the second ( smaller ) circle . If thre are some more circle and hexagons inscribed in the similar way as given above, then the ratio of each side of outermost hexagon ( largest one ) to that of the fourth ( smaller cone ) hexagon is ( fourth hexagon means the hexagon which is inside the third hexagon from the outside ):
If thre are some more circle and hexagons inscribed in the similar way as given above, then the ratio of each side of outermost hexagon ( largest one ) to that of the fourth ( smaller cone ) hexagon is ( fourth hexagon means the hexagon which is inside the third hexagon from the outside ):

A

a. 9:3√2

B

b. 16:9

C

c . 8:3√3

D

d. none of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Updated on:21/07/2023
|
Answer

Step by step video, text & image solution for A regular hexagon is inscirbed in a circle of radius R . Another circle is inscribed in the hexagon . Now another hexagon is inscribed in the second ( smaller ) circle . If thre are some more circle and hexagons inscribed in the similar way as given above, then the ratio of each side of outermost hexagon ( largest one ) to that of the fourth ( smaller cone ) hexagon is ( fourth hexagon means the hexagon which is inside the third hexagon from the outside ): by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.

Updated on:21/07/2023
Class 14MATHSMENSURATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A regular hexagon is inscirbed in a circle of radius R . Another circle is inscribed in the hexagon . Now another hexagon is inscribed in the second ( smaller ) circle .
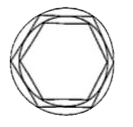
    ocr_image
    What is the sum of perimeters of both the hexagons ?

    A(2+√3)R
    B3(2+√3)R
    C3(3+√2)R
    Dnone of these

  • A regular hexagon is inscirbed in a circle of radius R . Another circle is inscribed in the hexagon . Now another hexagon is inscribed in the second ( smaller ) circle .
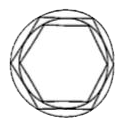
    ocr_image
    What is the ratio of area of inner circle to the outer circle ?

    A3:4
    B9:16
    C3:8
    Dnone of these

  • If a regular hexagon is inscribed in a circle of radius r , then its perimeter is :

    A6√3r
    B6r
    C3r
    D12r