PT is a tangent to a circle with centre O and radius 6cm. If PT is 8cm then length of OP is:
a.10cm
b. 12cm
c. 16 cm
d.none of these
The correct Answer is:A
To solve the problem step by step, we will use the properties of tangents and the Pythagorean theorem.
1. Understand the Problem: We have a circle with center O and radius 6 cm. PT is a tangent to the circle, and its length is 8 cm. We need to find the length of OP, where P is the point outside the circle.
2. Identify Key Points:
- O is the center of the circle.
- T is the point where the tangent PT touches the circle.
- The radius OT is perpendicular to the tangent PT at point T.
3. Draw a Right Triangle:
- We can visualize the situation as a right triangle OTP, where:
- OT is the radius (6 cm),
- PT is the tangent (8 cm),
- OP is the hypotenuse (which we need to find).
4. Apply the Pythagorean Theorem:
- According to the Pythagorean theorem, in a right triangle, the square of the length of the hypotenuse (OP) is equal to the sum of the squares of the lengths of the other two sides (OT and PT).
- The formula is:
OP2=OT2+PT2
5. Substitute the Known Values:
- We know OT = 6 cm and PT = 8 cm.
- Substitute these values into the equation:
OP2=62+82
6. Calculate the Squares:
- Calculate 62 and 82:
62=36
82=64
7. Add the Squares:
- Now, add the results:
OP2=36+64=100
8. Find the Length of OP:
- To find OP, take the square root of both sides:
OP=√100=10 cm
9. Conclusion:
- The length of OP is 10 cm.
Final Answer:
The length of OP is 10 cm.
---
- O is the center of the circle.
- T is the point where the tangent PT touches the circle.
- The radius OT is perpendicular to the tangent PT at point T.
- We can visualize the situation as a right triangle OTP, where:
- OT is the radius (6 cm),
- PT is the tangent (8 cm),
- OP is the hypotenuse (which we need to find).
- According to the Pythagorean theorem, in a right triangle, the square of the length of the hypotenuse (OP) is equal to the sum of the squares of the lengths of the other two sides (OT and PT).
- The formula is:
OP2=OT2+PT2
- We know OT = 6 cm and PT = 8 cm.
- Substitute these values into the equation:
OP2=62+82
- Calculate 62 and 82:
62=36
82=64
- Now, add the results:
OP2=36+64=100
- To find OP, take the square root of both sides:
OP=√100=10 cm
- The length of OP is 10 cm.
The length of OP is 10 cm.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - TEST OF YOUR LEARNING18videos
MENSURATION
- BOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - EXERCISE (LEVEL 1)55videos
MENSURATION
- BOOK - ARIHANT SSCCHAPTER - LOGARITHM EXERCISE - EXERCISE LEVEL 219videos
LOGARITHM
- BOOK - ARIHANT SSCCHAPTER - MIXED GRAPHEXERCISE - Higher Skill Level Questions15videos
MIXED GRAPH
Similar Questions
Knowledge Check
- Question 1 - Select One
PT is a tangent to a circle with centre O and radius 6cm. If PT is 8cm then length of OP is:
A10 cm.B12 cm.C16 cm.D9 cm. - Question 2 - Select One
AB is a tangent to a circle with centre O. If the radius at the circle is 7 cm and the length of AB is 24 cm, then what is the length (in cm) of OA?
A25B26C28D31 - Question 3 - Select One
PR is tangent to a circle, with centre O and radius 4 cm, at point Q. If ∠POR=90∘,OR=5cmand OP=203cm, then (in cm) the length of PR :
A3B163C233D253
In the given figure, PT is a tangent to the circle with centre O. If OT=6cm and OP=10cm, thcn find the length of tangent PT.
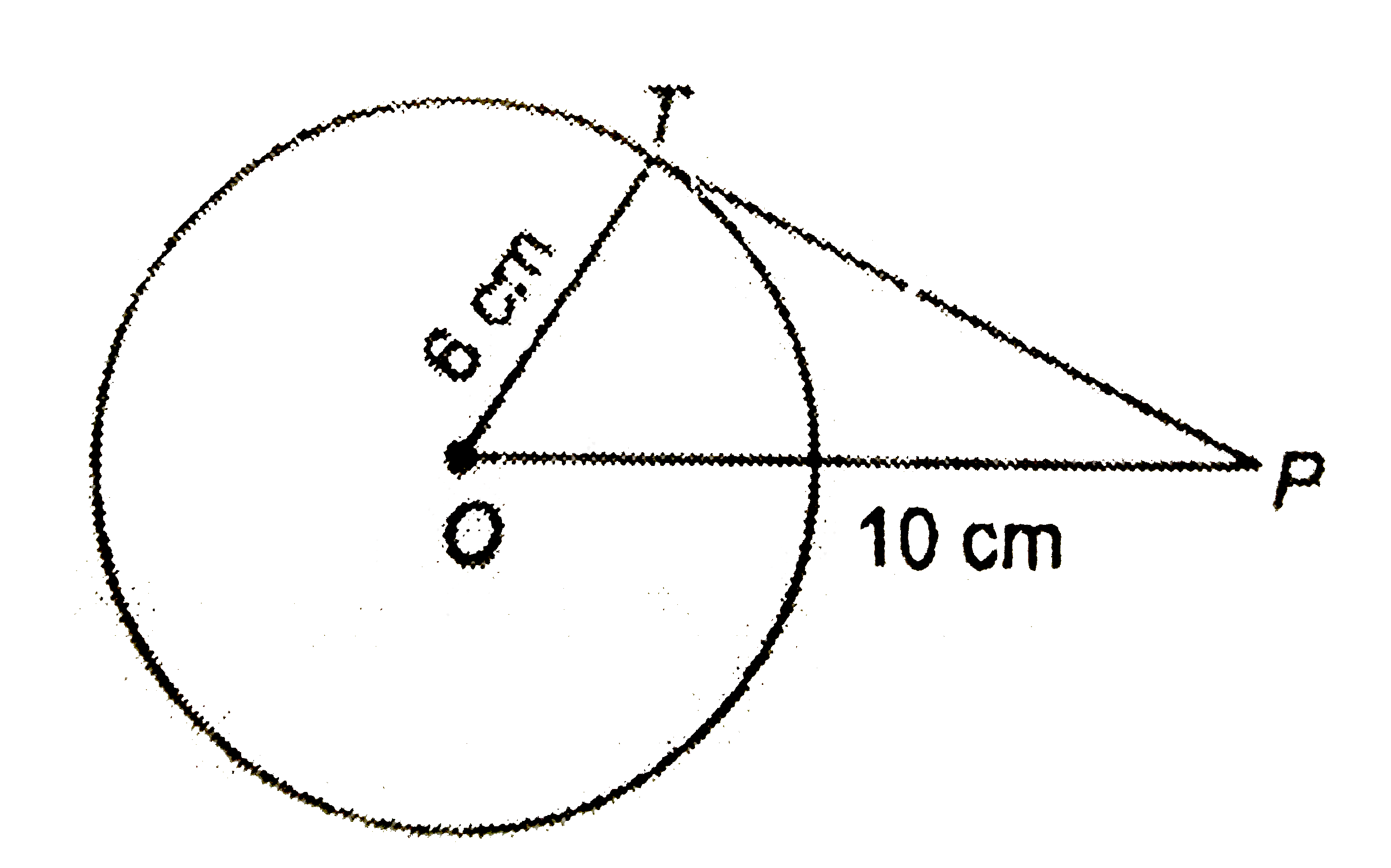 View Solution
View SolutionFind the length of the tangent to a circle with centre O and radius 6cm from a point P such that OP=10cm?
View Solution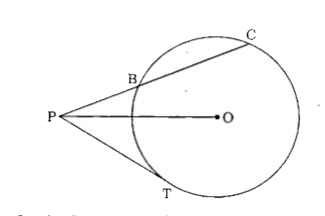
In the figure given above, PT is a tangent to a circle of radius 6 cm. If P is at a distance of 10 cm from the centre O and PB = 5 cm, then what is the length of the chord BC ?View SolutionIn the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
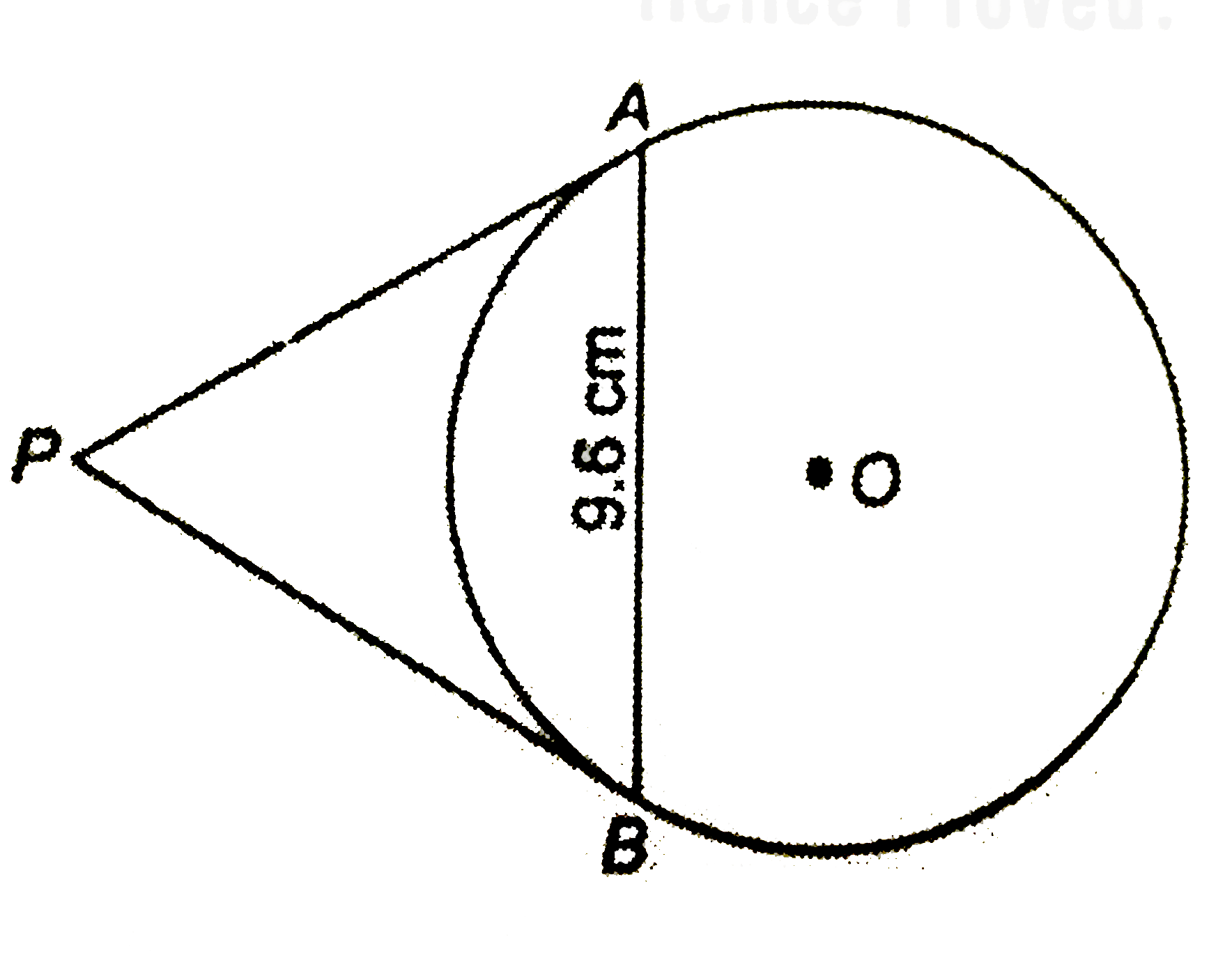 View Solution
View SolutionA and B invests Rs.8000 and Rs.9000 in a business. After 4 months, A withdraws half of his capital and 2 months later, B withdraws one-third of his capital. In what ratio should they share the profits at the end of the year ?
View Solution

