A (-3,2) and B(5,4) are the end points of a lline segment , find the coordinates of the mid points of the line segment :
(1,3)
(2,3)
(3,2)
(4,3)
The correct Answer is:A
To find the midpoint of the line segment with endpoints A(-3, 2) and B(5, 4), we will use the midpoint formula. The midpoint M of a line segment with endpoints (x1, y1) and (x2, y2) is given by the formula:
M=(x1+x22,y1+y22)
1. Identify the coordinates of points A and B:
- Point A has coordinates (-3, 2), so x1=−3 and y1=2.
- Point B has coordinates (5, 4), so x2=5 and y2=4.
2. Substitute the coordinates into the midpoint formula:
M=(−3+52,2+42)
3. Calculate the x-coordinate of the midpoint:
- First, calculate −3+5:
−3+5=2
- Now divide by 2:
22=1
4. Calculate the y-coordinate of the midpoint:
- First, calculate 2+4:
2+4=6
- Now divide by 2:
62=3
5. Combine the results to find the midpoint:
- The coordinates of the midpoint M are:
M=(1,3)
Final Answer:
The coordinates of the midpoint of the line segment AB are (1, 3).
---
- Point A has coordinates (-3, 2), so x1=−3 and y1=2.
- Point B has coordinates (5, 4), so x2=5 and y2=4.
M=(−3+52,2+42)
- First, calculate −3+5:
−3+5=2
- Now divide by 2:
22=1
- First, calculate 2+4:
2+4=6
- Now divide by 2:
62=3
- The coordinates of the midpoint M are:
M=(1,3)
The coordinates of the midpoint of the line segment AB are (1, 3).
Topper's Solved these Questions
- CO-ORDINATE GEOMETRYBOOK - ARIHANT SSCCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - INTRODUCTORY EXERCISE 21.2
35 Videos
- CLOCK AND CALENDARBOOK - ARIHANT SSCCHAPTER - CLOCK AND CALENDAREXERCISE - FAST TRACK PRACTICE
27 Videos
- COMPOUND INTERESTBOOK - ARIHANT SSCCHAPTER - COMPOUND INTERESTEXERCISE - EXERCISE C HIGHER SKILL LEVEL QUESTIONS
12 Videos
Similar Questions
Knowledge Check
A (-1, 4) and B(5, 4) are the end points of a line segment, find the coordinates of the mid points of the line segment :
A(2, 4)B(2, 3)C(3, 2)D(4, 3)A (-3,2) and B(5,4) are the end points of a lline segment ,find the co-ordinates of the point which divides AB in the ratio 2:3 :
A(15,145)B(2,3)C(15,3)D(3,12)
Plot the points A(1,-1) and B(4,5).
(i) Draw the line segment joining these points. Write the coordinates of a point on this line segment betwee the points A and B.
(ii) Extend this line segment and write the coordinates of a point on this line which lies outside the line segment AB.
View SolutionShow that the mid-point of the line segment joining the points (5, 7) and (3, 9) is also the mid-point of the line segment joining the points (8, 6) and (0, 10) .
View SolutionFind mid point of a line segment of length 6.8 cm.
View SolutionIf the vertices of a triangle are (0,0,0),(1,−2,1) and (3,4,5), then the coordinates of the mid point of the line segment joining the orthocentre and the circumcentre is
View SolutionIn Figure, lm and M is the mid-point of the line segment AB. Prove that M is also the mid-point of any line segment CD having its end-points on l and m respectively.
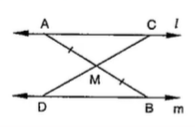
View SolutionIn figure l||m and M is the mid-point of the line segment AB. Prove that M is also the mid-point of line segment CD.

View Solution