एक -कण V बोल्ट विभवान्तर से त्वरित होकर किसी नाभिक से टकराता है। यदि नाभिक की परमाणु संख्या Z हो तो सिद्ध कीजिए कि -कण की नाभिक से निकटतम दूरी है-
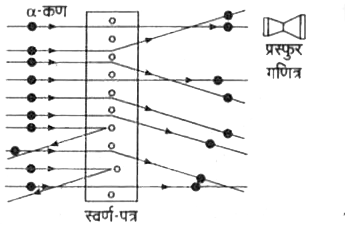
रदरफोर्ड का -कणों के प्रकीर्णन का प्रयोग-सन् 1911 ई० में रदरफोर्ड ने परमाणु की संरचना जानने के लिए एक प्रयोग किया। इसमें रदरफोर्ड ने रेडियोऐक्टिव तत्व पोलोनियम से अधिक गतिज ऊर्जा से निकलने वाली -किरणों के एक बारीक किरण पुंज को एक बहुत पतले स्वर्ण-पत्र पर गिराया तथा पूरे प्रबन्ध को निर्वात में रखकर देखा कि स्वर्ण-पत्र में से गुजरते हुए ये -कण विभिन्न दिशाओं में विक्षेपित हो जाते हैं। पूरे प्रबन्ध को निर्वात में इसलिए रखा जिससे कि कणों की वायु के कणों से कोई टक्कर न हो। -कणों । प्रस्फुर के अपने मार्ग से विक्षेपित होने कीcगणित्र इस क्रिया को प्रकीर्णन कहते हैं। से अलग-अलग कोणों : पर प्रकीर्णित व -कणों को एक प्रस्फुर - गणित्र द्वारा गिना गया। रदरफोर्ड ने अपने इस प्रयोग से निम्नलिखित स्वर्ण-पत्र महत्त्वपूर्ण तथ्य प्राप्त किए-.
अधिकांश -कण स्वर्ण-पत्र से बिना विक्षेपित हुए सीधे पार निकल जाते हैं। इससे रदरफोर्ड ने निष्कर्ष निकाला कि परमाणु का अधिकांश भाग अन्दर से खोखला होता है।
2.कुछ-कण, अपने मार्ग से छोटे कोण ( से कम) बनाते हुए विक्षेपित हो जाते हैं। चूँकि कण धनावेशित हैं, अत: ये किसी धनावेशित वस्तु से ही विक्षेपित हो सकते हैं। इस आधार पर रदरफोर्ड ने यह माना कि परमाणु का सम्पूर्ण धनावेश परमाणु के अन्दर एक छोटे से स्थान पर केन्द्रित रहता है।
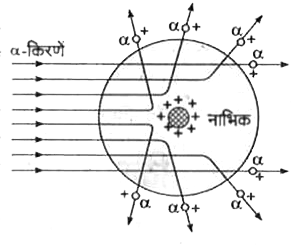
कुछ -कण, अपने मार्ग से अधिक कोण ( से अधिक) पर प्रकीर्णित होकर वापस लौट आते हैं (चित्र देखिए)। इससे ज्ञात होता है कि जब धनावेशित -कण स्वर्ण-पत्र के परमाणुओं में से गुजरते हैं तो कुछ -कणों पर इतना अधिक प्रतिकर्षण बल लगता है कि वह अपने मार्ग से अधिक कोण पर प्रकीर्णित होकर वापस लौट आता है। इससे रदरफोर्ड ने यह निष्कर्ष निकाला कि परमाणु का बनावेश उसके केन्द्रीय भाग के एक अति सूक्ष्म स्थान में संकेन्द्रित रहता है, जिसे नाभिक कहते हैं।
चित्र से स्पष्ट है कि -कण नाभिक के जितने समीप जाता है उस पर उतना ही अधिक प्रतिकर्षण बल लगता है और वह उतने ही बड़े कोण से विक्षेपित होता है। रदरफोर्ड ने -कणों की नाभिक के निकटतम पहुँच की दूरी (नाभिक की त्रिज्या) की गणना की और इसे लगभग मीटर पाया जो कि परमाणु की त्रिज्या मीटर) की तुलना में बहुत कम है। क्योकि परमाणु के आकार की तुलना में नाभिक अत्यन्त छोटा होता है, अत: किसी कण की नाभिक के समीप पहुंचने की सम्भावना बहुत कम होती है। इस प्रकार बड़े कोणों पर प्रकीर्णित (ऐल्फा) कणों की संख्या बहुत कम होती है।
4. जब कोई -कण, स्वर्ण-पत्र के परमाणुओं में से गुजरता है तो उस पर नाभिक द्वारा लगाया गया प्रतिकर्षण बल, (कूलॉम के नियमानुसार) नाभिक से दूरी के वर्ग के व्युत्क्रमानुपाती होता है। परमाणु से गुजरते समय जो कण नाभिक से दूर रहता है उस पर प्रतिकर्षण बल इतना कम लगता है कि वह बिना विक्षेप के अपने मार्ग पर चला जाता है, परन्तु जो कण नाभिक के समीप से गुजरता है, उस पर अधिक प्रतिकर्षण बल लगता है और वह उतने ही बड़े कोण से प्रकीर्णित हो जाता है।
कूलॉम के नियम से रदरफोर्ड ने विभिन्न कोणों पर प्रकीर्णित होने वाले कणों का परिकलन करके पाया कि कूलॉम का नियम परमाण्वीय दूरियों के लिए भी होता है।
5. रदरफोर्ड ने अपने प्रयोग द्वारा विभिन्न धातुओं के नाभिकों में उपस्थित धनावेश की मात्राओं का भी अनुमान लगाया। उन्होंने कणों को भिन्न-भिन्न धातुओं (जैसे-सोना, चाँदी आदि) की पतली पतों पर गिराकर, एक निश्चित कोण पर प्रकीर्णित होने वाले कणों को गिना और देखा कि यह संख्या भिन्न-भिन्न धातुओं के लिए भिन्न-भिन्न आती है। इससे उन्होंने निष्कर्ष निकाला कि भिन्न-भिन्न धातुओं के नाभिकों में धनावेशों की मात्राएं भिन्न-भिन्न होती हैं। इस प्रकार नाभिक में जितना अधिक धनावेश होगा वह .कण को उतने ही अधिक बल से प्रतिकर्षित करेगा तथा -कण अपने मार्ग से उतना ही अधिक विक्षेपित होगा।
नाभिक से निकटतम दूरी--कण पर आवेश- +2e.
V बोल्ट विभवान्तर से त्वरित करने पर -कण की गतिज ऊर्जा = 2 ev
नाभिक से निकटतम दूरी पर-कण की गतिज ऊर्जा = कण व नाभिक निकाय की स्थितिज ऊर्जा
या
मी
रदरफोर्ड परमाणु मॉडल की कमी–रदरफोर्ड परमाणु मॉडल में निम्नलिखित कमियाँ थीं-
1. परमाणु के स्थायित्व के सम्बन्ध में (Stability of the Atom)चूँकि नाभिक के चारों ओर घूमते इलेक्ट्रॉनों में अभिकेन्द्र त्वरण होता है। वैद्युत गति विज्ञान के अनुसार त्वरित आवेशित कण वैद्युत-चुम्बकीय तरंगों के रूप में लगातार ऊर्जा उत्सर्जित करता है अत: नाभिक के चारों ओर विभिन्न कक्षाओं में घूमते हुए इलेक्ट्रॉनों से भी वैद्युत-चुम्बकीय तरंगों का उत्सर्जन लगातार होना चाहिए। इस प्रकार इलेक्ट्रॉनों की ऊर्जा का ह्रास होने से उनके वृत्तीय मार्ग की त्रिज्या लगातार घटती जानी चाहिए और अन्त में इलेक्ट्रॉन नाभिक में गिर जाने चाहिए। इस प्रकार परमाणु स्थायी नहीं रह सकता।
2. रेखीय स्पेक्ट्रम की व्याख्या के सम्बन्ध में (Explanation of Linear Spectrum)-रदरफोर्ड मॉडल के अनुसार इलेक्ट्रॉन सभी सम्भव त्रिज्याओं के वृत्तीय मार्ग में घूम सकते हैं अतः उन्हें सभी तरंगदैर्घ्य की वैद्युत-चुम्बकीय तरंगें उत्सर्जित करनी चाहिए अर्थात् इन तरंगों से प्राप्त स्पेक्ट्रम संतत (continuous) होना चाहिए, परन्तु प्रयोगों द्वारा परमाणुओं के स्पेक्ट्रम प्राय: संतत न होकर, रेखीय होते हैं अर्थात् उनमें कुछ निश्चित आवृत्तियों की ही तरंगें प्राप्त होती हैं। इस प्रकार रदरफोर्ड मॉडल, रेखीय स्पेक्ट्रम की व्याख्या करने में असफल रहा।
Similar Questions
रिक्त स्थानों की पूर्ति कीजिए -
मूल बिन्दु 0 से समतल →r.→N=d की दूरी ............... है।
View Solutionनाभिक अध्याय से महत्वपूर्ण प्रश्न
View Solutionनाभिक से दूरी पर, अनंतसूक्ष्म मोटाई dr के गोलीय कोश में हाइड्रोजन परमाणु के 1s इलेक्ट्रॉन के पाए जाने की प्रायिकता P है। इस कोश का आयतन 4rr2 dr है। r पर P की निर्भरता का गुणात्मक रेखाचित्र है-
View Solutionयदि हाइड्रोजन परमाणु का एक इलेक्ट्रॉन लाइमन श्रेणी में चतुर्थ उतेजित अवस्था से आद्य अवस्था में गति करता है तो स्पेक्ट्रमी रेखाओं की कूल संख्या ज्ञात कीजिए?
View Solutionसमान विभवांतर के माध्यम से त्वरित हुए alpha कण और प्रोटॉन के लिए तरंग दैर्ध्य के अनुपात की गणना कीजिए।
View Solutionएक alpha - कण, कॉपर के नाभिक (Z=29) के लक्ष्य की ओर इस प्रकार से उपगमन करता है। कि संघट्ट प्राचल का मान शून्य होता है। निकटतम उपगमन की दूरी होगी:
View Solutionरेडियो नाभिक 90234Th के दो क्रमिक β -क्षय के बाद एक -क्षय के माध्यम से एक नया रेडियो नाभिक प्राप्त किया जाता है। परिणामी रेडियो नाभिक का परमाणु क्रमांक और द्रव्यमान संख्या क्रमश: है:
View Solutionपरमाणु का नाभिक गोलाकार होता है। नाभिक की त्रिज्या और द्रव्यमान संख्या A के बीच संबंध 1.25×10−13×A13cm द्वारा दिया गया है। यदि परमाणु की त्रिज्या एक A है और द्रव्यमान संख्या 64 है, तब नाभिक द्वारा ग्रहण किये गए परमाण्विक आयतन का प्रभाज (x)×10−13 है। x की गणना कीजिए।
View Solution
