A substance has critical angle of 45∘ for yellow light. What is its refractive index ?
To find the refractive index of a substance given its critical angle, we can use Snell's law and the definition of the critical angle.
1. Understand the Concept of Critical Angle:
The critical angle (θc) is the angle of incidence in the denser medium (substance) at which the angle of refraction in the less dense medium (air) is 90 degrees.
2. Use the Formula for Critical Angle:
The relationship between the critical angle and the refractive indices of the two media is given by:
sin(θc)=μ1μ2
where:
- θc is the critical angle,
- μ1 is the refractive index of the denser medium (substance),
- μ2 is the refractive index of the less dense medium (air).
3. Identify the Refractive Index of Air:
The refractive index of air (μ2) is approximately 1.
4. Substitute the Given Values:
Given that the critical angle (θc) is 45∘, we can calculate sin(45∘):
sin(45∘)=1√2
5. Set Up the Equation:
Plugging the values into the critical angle formula:
1√2=μ11
This simplifies to:
μ1=1√2
6. Calculate the Refractive Index:
To find the refractive index of the substance (μ1), we take the reciprocal:
μ1=√2
7. Final Answer:
The refractive index of the substance is:
μ1=√2≈1.414
Summary:
The refractive index of the substance with a critical angle of 45∘ for yellow light is √2.
The critical angle (θc) is the angle of incidence in the denser medium (substance) at which the angle of refraction in the less dense medium (air) is 90 degrees.
The relationship between the critical angle and the refractive indices of the two media is given by:
sin(θc)=μ1μ2
where:
- θc is the critical angle,
- μ1 is the refractive index of the denser medium (substance),
- μ2 is the refractive index of the less dense medium (air).
The refractive index of air (μ2) is approximately 1.
Given that the critical angle (θc) is 45∘, we can calculate sin(45∘):
sin(45∘)=1√2
Plugging the values into the critical angle formula:
1√2=μ11
This simplifies to:
μ1=1√2
To find the refractive index of the substance (μ1), we take the reciprocal:
μ1=√2
The refractive index of the substance is:
μ1=√2≈1.414
The refractive index of the substance with a critical angle of 45∘ for yellow light is √2.
Topper's Solved these Questions
- BOOK - MBD -HARYANA BOARDCHAPTER - OPTICSEXERCISE - SHORT ANSWER TYPE QUESTIONS46videos
OPTICS
- BOOK - MBD -HARYANA BOARDCHAPTER - OPTICSEXERCISE - LONG ANSWER TYPE QUESTIONS18videos
OPTICS
- BOOK - MBD -HARYANA BOARDCHAPTER - MODEL TEST PAPER - 2EXERCISE - SET - D ( LONG ANSWER TYPE QUESTIONS)4videos
MODEL TEST PAPER - 2
- BOOK - MBD -HARYANA BOARDCHAPTER - PRINCIPLES OF COMMUNICATIONEXERCISE - Objective Type Questions19videos
PRINCIPLES OF COMMUNICATION
Similar Questions
A ray of light falls on a glass slab at an incident angle of 45∘ and refracted at angle of 30∘.
What is the refractive index of the glass with respect to air ?View SolutionA ray of light falls on a material body at an incident angle of 30∘ and refracted at angle 60∘.
What is the refractive index of the material?View Solution
Knowledge Check
- Question 1 - Select One
Light is incident on a substance of refractive index √2 at an angle of 45∘. What is the ratio of width of beam in air to the medium ?
A√3:√2B1:√15C1:2√2D√2:√3 - Question 2 - Select One
A glass slab has a critical angle of 30∘ when placed in air. What will be the critical angle when it is placed in liquid of refractive index 6/5?
A45∘B37∘C53∘D60∘ - Question 3 - Select One
A thin prism produces an angular dispersion of 24. If the refracting angle of the prism is 3∘ , and the refractive index of the material of the prism for red colour is 1.55 . What is the refractive index of its material for violet light ?
A1.55B1.61C1.683D1.653
As shown in Fig. PQ is a ray incident on prism ABC. Show the corresponding refracted and emergent rays. The critical angle for the material of the prism is 45∘. What is refractive index of the material of prism ?
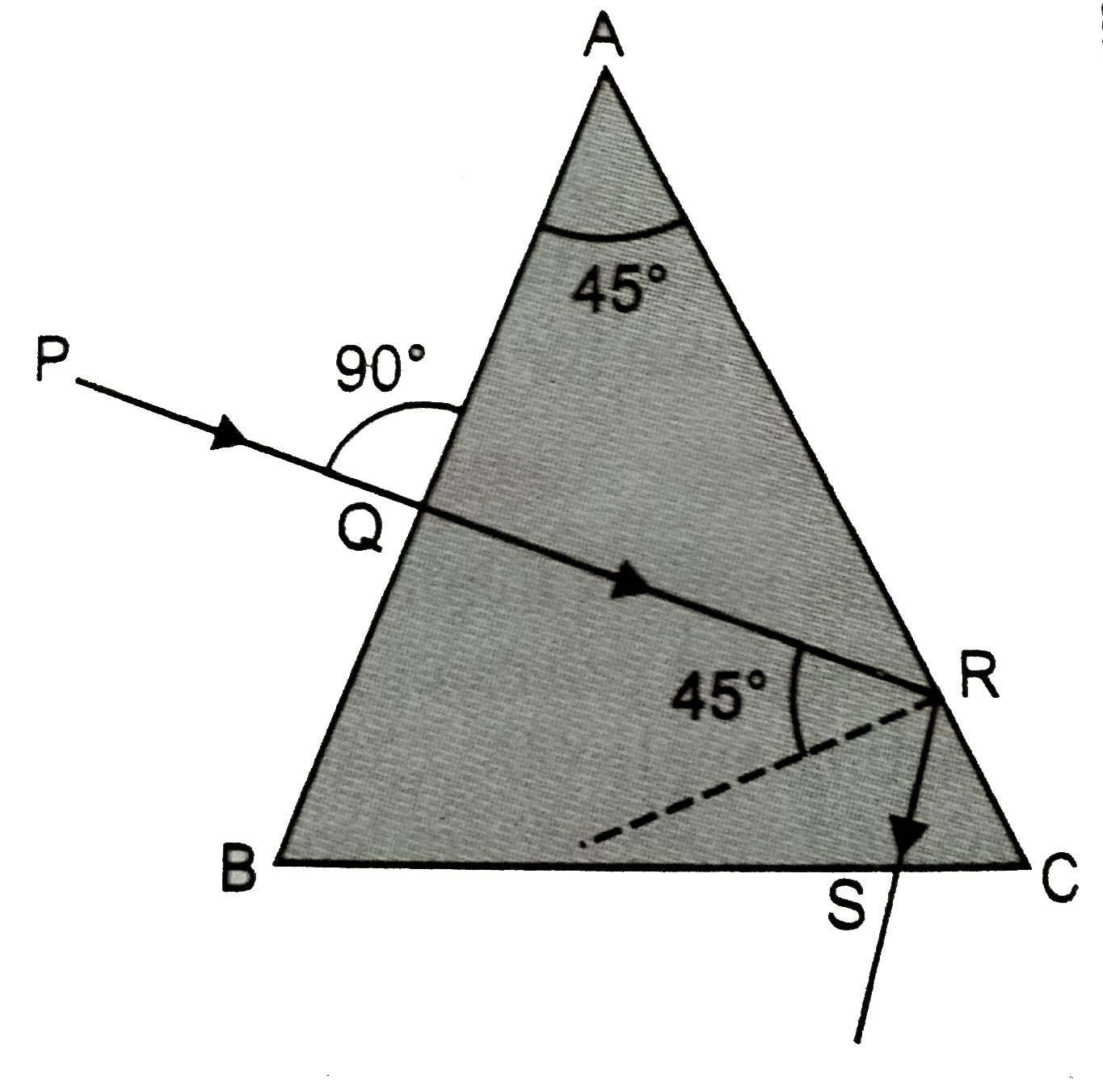 .View Solution
.View SolutionThe critical angle of a for a medium is 45∘. What is its polarising angle.
View SolutionThe critical angle for water is 48.2∘. Find is refractive index.
View SolutionA ray of light falls on a material body at an incident angle 60∘ and refracted at angle 30∘.
What is the refractive index of the material?View SolutionCalculate the critical angle for a pair of media, water and glass. Given refractive index of glass and water is 1.45 and 1.33 respectively.
View Solution

