Question

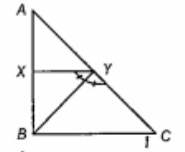
In a $\Delta ABC$, a line PQ parallel to BC cuts AB at P and AC at Q. If BQ bisects $\angle PQC$, then which one of the following relation is always true :

Options

A. `BC=CQ`
B. `BC=BQ`
C. `BCneCQ`
D. `BCneBQ`

Answer

A

Explanation

To solve the problem, we will analyze the given triangle $$\Delta ABC$$ and the line $$PQ$$ that is parallel to $$BC$$. We will also use the information that $$BQ$$ bisects $$\angle PQC$$.

1. Draw Triangle ABC:
Start by sketching triangle \( ABC \) with vertices \( A \), \( B \), and \( C \).

Hint: Label the vertices clearly to avoid confusion later.

2. Draw Line PQ Parallel to BC:
Draw line \( PQ \) such that it is parallel to side \( BC \) of triangle \( ABC \). Mark the intersection points where \( PQ \) meets \( AB \) at point \( P \) and \( AC \) at point \( Q \).

Hint: Remember that parallel lines create corresponding angles that are equal.

3. Identify Angles:
Since \( BQ \) bisects \( \angle PQC \), let \( \angle PQB = \theta \) and \( \angle QBC = \theta \) as well. Therefore, \( \angle PQC = 2\theta \).

Hint: Use the property of angle bisectors to set up relationships between the angles.

4. Use Alternate Interior Angles:
Because \( PQ \) is parallel to \( BC \), we can say that \( \angle QBC = \angle PQC \). Thus, \( \angle QBC = \theta \).

Hint: Recall that alternate interior angles are equal when two lines are parallel.

5. Establish Isosceles Triangle:
Since \( \angle PQB = \theta \) and \( \angle QBC = \theta \), triangle \( BQC \) is isosceles with \( BQ = BC \).

Hint: In an isosceles triangle, the angles opposite to equal sides are equal.

6. Conclude the Relationship:
From the isosceles triangle \( BQC \), we can conclude that \( BC = CQ \).

Hint: This conclusion is based on the properties of isosceles triangles.

7. Choose the Correct Option:
Among the options provided, the correct relationship that is always true is \( BC = CQ \).

Hint: Verify that this conclusion aligns with the options given in the problem.

Final Answer:
The relation that is always true is \( BC = CQ \).