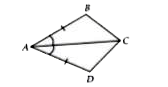
In the given figure, AB = BC and ∠BAC=15∘,AB=10cm. Find the area of ΔABC:
50cm2
40cm2
25cm2
32cm2
The correct Answer is:C
Step by step video, text & image solution for In the given figure, AB = BC and angleBAC = 15^(@), AB=10cm. Find the area of DeltaABC: by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.3
Explore 28 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.4
Explore 10 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.1
Explore 45 Videos
- FUNDAMENTALS Book:ARIHANT SSCChapter:FUNDAMENTALS Exercise:TEST OF YOU - LEARNING - 2
Explore 40 Videos
- HCF AND LCMBook:ARIHANT SSCChapter:HCF AND LCMExercise:Exercise Higher Skill Level Questions
Explore 18 Videos
Similar Questions
Knowledge Check
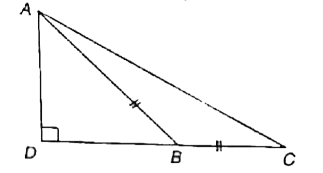
In the given figure AD=15cm,AB=20cmandBC=CD=25cm. Find the area of □ABCD:
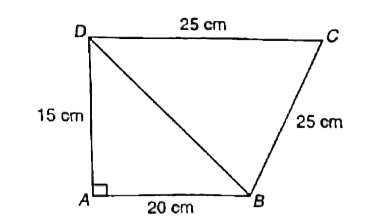 A254(24+25√3)cm2B24(25+24√3)cm2C252(24+25√3)cm2Dnone of these
A254(24+25√3)cm2B24(25+24√3)cm2C252(24+25√3)cm2Dnone of theseIn the given figure AB = 12, AC = 15 cm and AD = 6 cm. BC∣∣DE, find the length of AE
 A6 cmB7.5 cmC9 cmD10 cm
A6 cmB7.5 cmC9 cmD10 cm
In the given figure, AB = AD and ∠BAC=∠DAC. Then
(ii) BC = ____.

View SolutionIn ΔABC,∠ABC=150∘,AD⊥BC,AB=20cm. Find height of ΔABC.
View SolutionIn the given figure, ΔABC is right angled at A. Find the area of the shaded region if AB = 6 cm, BC = 10 cm and O is the centre of the incricle of ΔABC. (Use π=3.14)

View SolutionIn the given figure, ΔABC is right angled at A. Find the area of the shaded region if AB=6cm,BC=10cm andO is the centre of the incircle of ΔABC. [Take π=3.14]

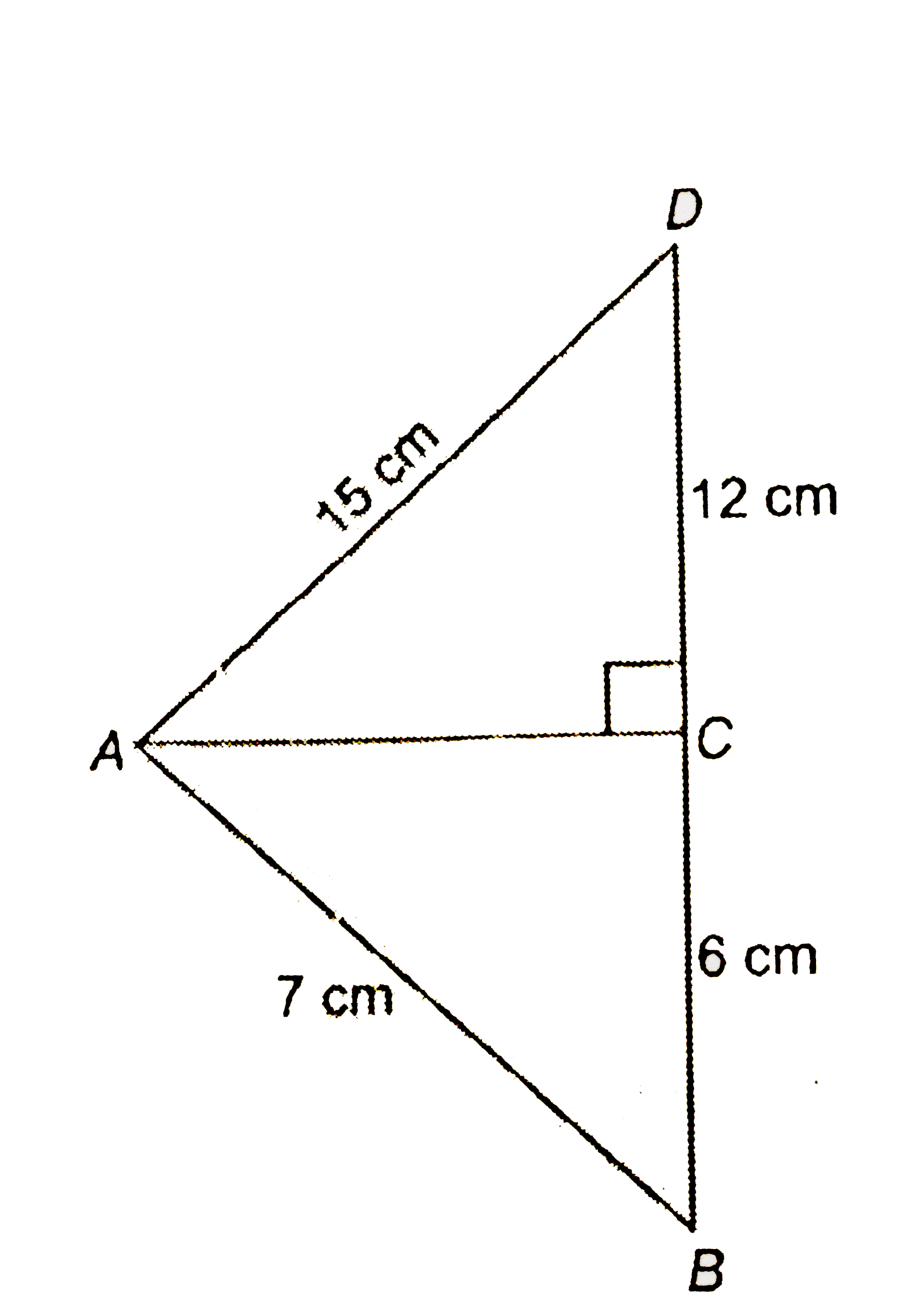
View SolutionIn the given figure ∠ACD=90∘
AD=15cm,DC=12cm,AB=7cm and BC=6cm.
Find the are of the shaded region.
View SolutionIn the given figure , ∠DBC=65∘,∠BAC=35∘ and AB=BC, then the measure of ∠ECD is equal to:
View Solution