If a∈R and the equation −3(x−[x])2+2(x−[x])+a2=0 (where [x] denotes the greatest integer ≤x) has no integral solution, then all possible values of a lie in the interval: (1) (-2,-1) (2) (∞,−2)∪(2,∞) (3) (−1,0)∪(0,1) (4) (1,2)
(−1,0)∪(0,1)
(1,2)
(−2,−1)
(−∞,−2)∪(2,∞)
a2=3t2−2t, where t={x}∈[0,1)
∴a2=3t(t−2/3)
Graph of f(t)=3t(t−2/3) is as shown in the following figure.
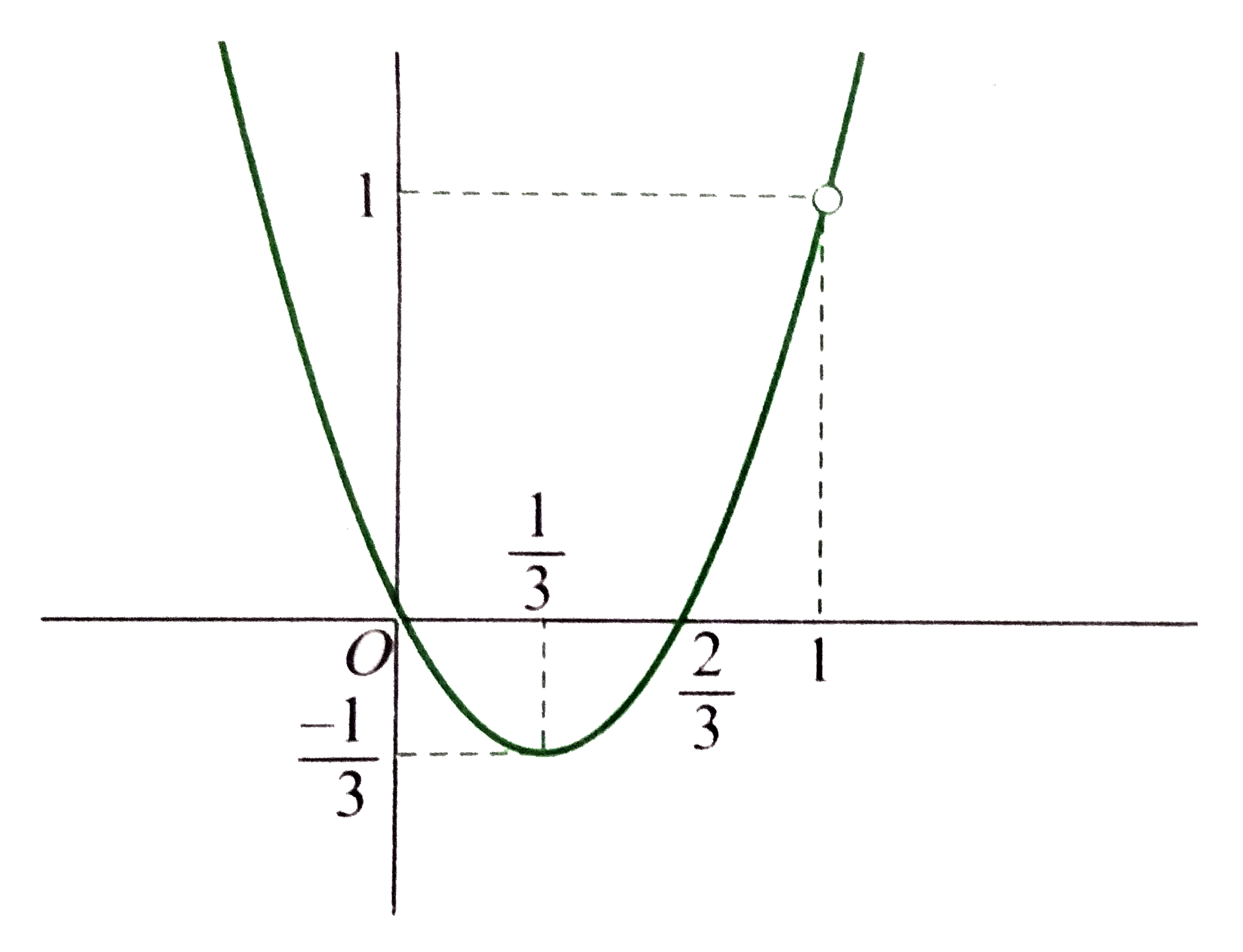
Clearly, from graph
0<a2<1
ora∈(−1,0)∪(0,1)
Similar Questions
If a∈R and the equation −3(x−[x])2+2(x−[x])+a2=0 (where [x] denotes the greatest integer x) has no integral solution, then all possible values of a lie in the interval (1) (−1,0)∪(0,1) (2) (1, 2) (3) (−2,−1) (4) (−∞,−2)∪(2,∞)
View SolutionIf a∈R and the equation −3(x−[x])2+2(x−[x])+a2=0 (where [x] denotes the greatest integer x) has no integral solution, then all possible values of a lie in the interval (1) (−1,0)∪(0,1) (2) (1, 2) (3) (−2,−1) (4) (−∞,−2)∪(2,∞)
View Solution
Knowledge Check
If a ∈ R and the equation (a−2)(x−[x])2+2(x−[x])+a2=0 (where [x] denotes the greatest integer function) has no integral solution and has exactly one solution in (2, 3), then a lies in the interval
A(−1,2)B(0, 1)C(−1,0)D(2, 3)If f(x)={∣∣1−4x2∣∣,0≤x<1[x2−2x],1≤x<2, where [] denotes the greatest integer function, then
Af(x) is continuous for all x∈[0,2)Bf(x) is differentiable for all x∈[0,2)−{1}Cf(X) is differentiable for all x∈[0,2)−{12,1}DNone of these
If a ∈ R and the equation (a−2)(x−[x])2+2(x−[x])+a2=0 (where [x] denotes the greatest integer function) has no integral solution and has exactly one solution in (2, 3), then a lies in the interval
View SolutionThe solution set of the inequality max {1−x2,|x−1|}<1 is (−∞,0)∪(1,∞) (b) (−∞,0)∪(2,∞) (0,2) (d) (0,2)
View SolutionThe domain of f(x)=log12log4log3[x−λ]2 (where [ ] denotes the greatest integer function) is (−∞,2]∪[6,∞) then the value of λ is
View SolutionThe solution set of the inequality max {1−x2,|x−1|}<1 is (−∞,0)∪(1,∞) (b) (−∞,0)∪(2,∞) (0,2) (d) (0,2)
View SolutionIf [x+[x]]≤8 where [.] denotes the greatest integer function then x belongs to 1) (−∞,1) 2) (−∞,4) 3) (−∞,5) 4) (0,2)
View SolutionIf [x +[2x]] < 3, where[.] denotes the greatest integer function, then x is: 1.) [0,1) 2.) (−∞,32] 3.)(1,∞) 4.) (−∞,1)
View Solution
