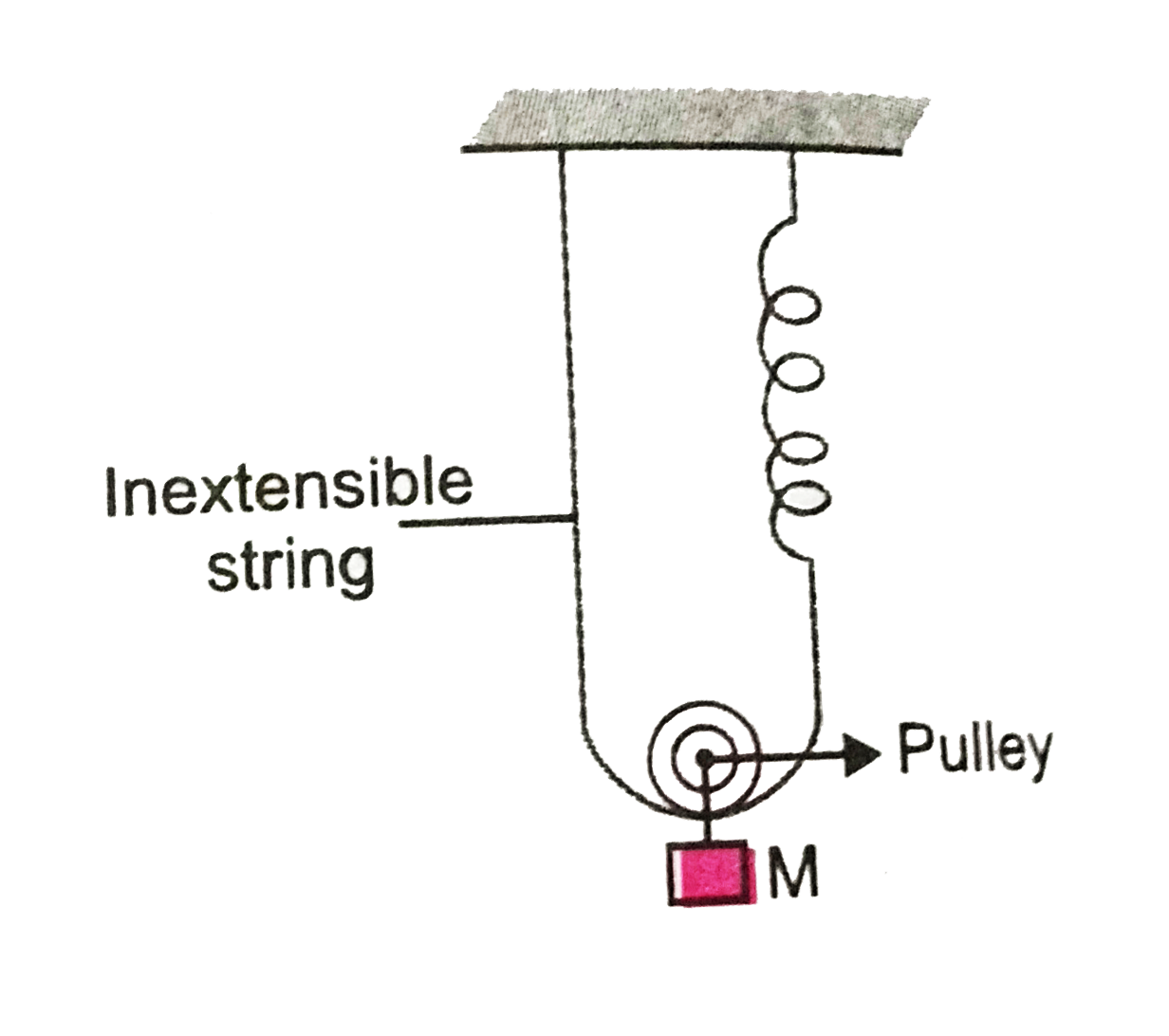
Find the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

Let spring constant of the spring be k, When the mass M moves down by, l, then the spring will extend 2l (because each side will expand by length l).
So restoring force
F=−2k(2l)=−4kl
In equilibrium position.
Mg=4kl
On pulling the mass down by y, the restoring force F will be
F−2k(2l+2y)
Net restoring force,
f=F.=F=−4kl−4ky−(−kl)
or f=−4ky
So the motion will be S.H.M.
And its time period, T=2π√mk=2π√M4k.
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - HOTS (Higher Order Thinking Skills & Advanced Level)
11 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Revision Exercises (Very Short Answer Questions)
37 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT Exemplar Problems Subjective Question (Very short Answer Type Questions )
10 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
Find the time period of mass M when displaced from its equilibrium position and then reelased for the system shown in figure.
View SolutionA particle of mass m is suspended from a fixed point O by a string length l.At t=0, it is displaced from its equilibrium position and released.If T is the tension in the string with time t, then the correct graph is
View Solution
Knowledge Check
A small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
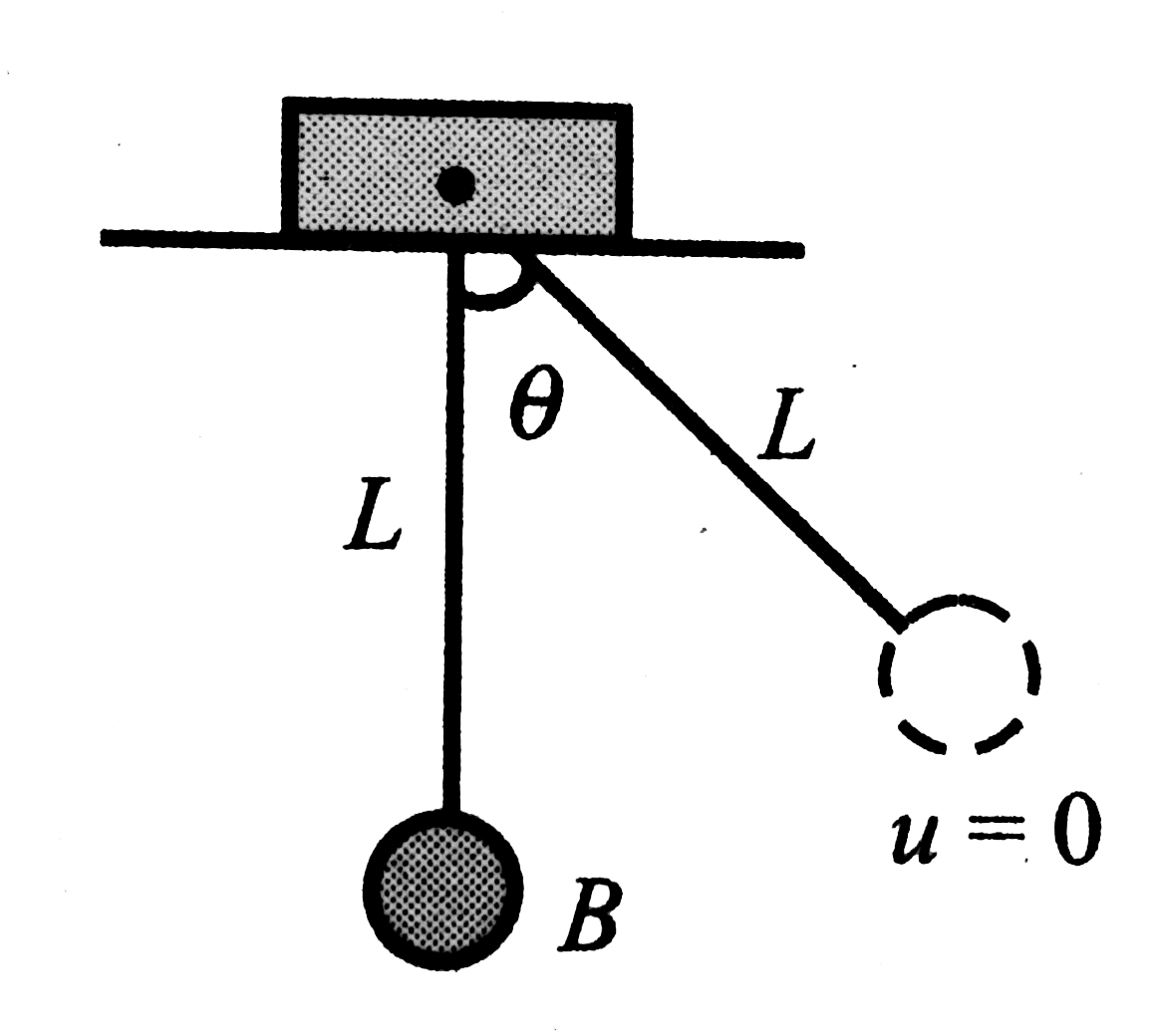 The displacement of centre of mass of A+B system till the string becomes vertical is AzeroBL(1−cosθ)CL2(1−cosθ)Dnone of these
The displacement of centre of mass of A+B system till the string becomes vertical is AzeroBL(1−cosθ)CL2(1−cosθ)Dnone of theseA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
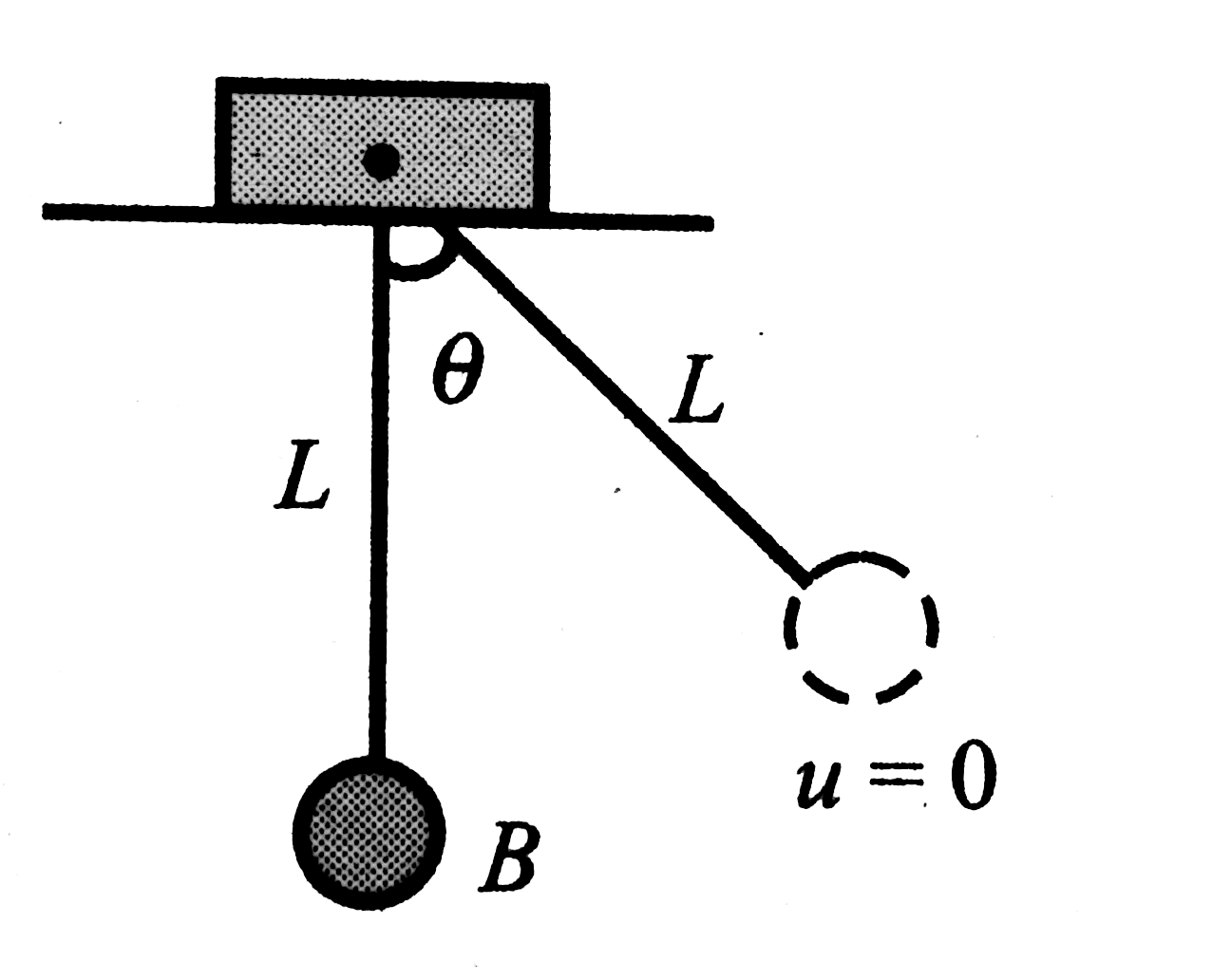
Tension in string when it is vertical, isAmgBmg(2−cosθ)Cmg(3−2cosθ)Dnone of theseFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
 A2π√mKBπ√m4KCπ√mKD4π√mK
A2π√mKBπ√m4KCπ√mKD4π√mK
A mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximu speed of the trolley is
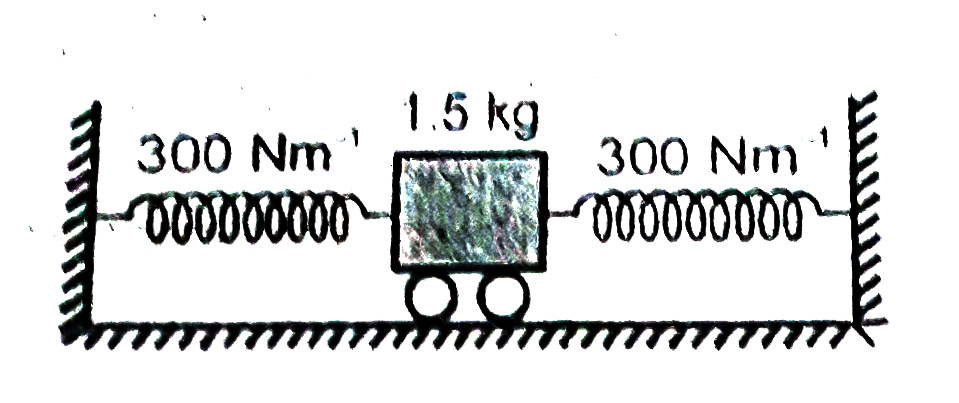
View SolutionFigure-1 to Figure -4 shows four different spring arrangements . Mass m in each arrangement is displacement from its equilibrium position and released Neglec mass of the springs. Choose the correct statement (s)

View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

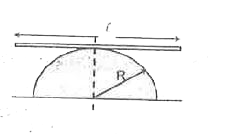
View SolutionA uniform plank of length l and mass m is balanced on a fixed semi-circular plate of radius R as shown in the figure. If the plank is tilted slightly from its equilibrium position, and released, prove that it will execute S.H.M find the period of its oscillation.
View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.

The displacement of block when equilibrium position is
View Solution
