The displacement of a damped harmonic oscillator is given by x(t)=e−0.1tcos(10πt+ϕ). Here t is in seconds
The time taken for its amplitude of vibration to drop to half of its initial is close to :
4s
7s
13s
27s
The correct Answer is:B
To find the time taken for the amplitude of the damped harmonic oscillator to drop to half of its initial value, we can follow these steps:
Step 1: Identify the initial amplitude
The displacement of the damped harmonic oscillator is given by:
x(t)=e−0.1tcos(10πt+ϕ)
Here, the amplitude of the oscillation is given by the term e−0.1t. At t=0, the initial amplitude A0 is:
A0=e0=1
Step 2: Set up the equation for half the amplitude
We want to find the time t when the amplitude drops to half of its initial value:
A(t)=A02
Substituting the expression for amplitude, we have:
e−0.1t=12
Step 3: Solve for t
To solve for t, take the natural logarithm of both sides:
−0.1t=ln(12)
Now, rearranging gives:
t=−ln(12)0.1
Step 4: Calculate t
Using the property of logarithms, we know that:
ln(12)=−ln(2)
Thus, we can rewrite the equation as:
t=ln(2)0.1
Now, using the approximate value of ln(2)≈0.693:
t≈0.6930.1=6.93 seconds
Final Answer
The time taken for the amplitude of vibration to drop to half of its initial value is approximately 6.93 seconds.
---
The displacement of the damped harmonic oscillator is given by:
x(t)=e−0.1tcos(10πt+ϕ)
A0=e0=1
We want to find the time t when the amplitude drops to half of its initial value:
A(t)=A02
Substituting the expression for amplitude, we have:
e−0.1t=12
To solve for t, take the natural logarithm of both sides:
−0.1t=ln(12)
Now, rearranging gives:
t=−ln(12)0.1
Using the property of logarithms, we know that:
ln(12)=−ln(2)
Thus, we can rewrite the equation as:
t=ln(2)0.1
t≈0.6930.1=6.93 seconds
The time taken for the amplitude of vibration to drop to half of its initial value is approximately 6.93 seconds.
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (JEE (Advanced) For IIT Entrance)
7 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Multiple choice question)
11 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Multiple choice questions) AIPMT/NEET other State Boards for Medical Entrance
14 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
The equation of a simple harmonic motion is given by x=6sin10t+8cos10t, where x is in cm, and t is in seconds. Find the resultant amplitude.
View SolutionFor the damped oscillator shown in Fig, the mass of the block is 200g,k=80Nm−1 and the damping constant b is 40gs−1 Calculate
(a) The period of oscillation
(b) Time taken for its amplitude of vibrations to drop to half of its initial values
(c) The time for the mechanical energy to drop to half initial values
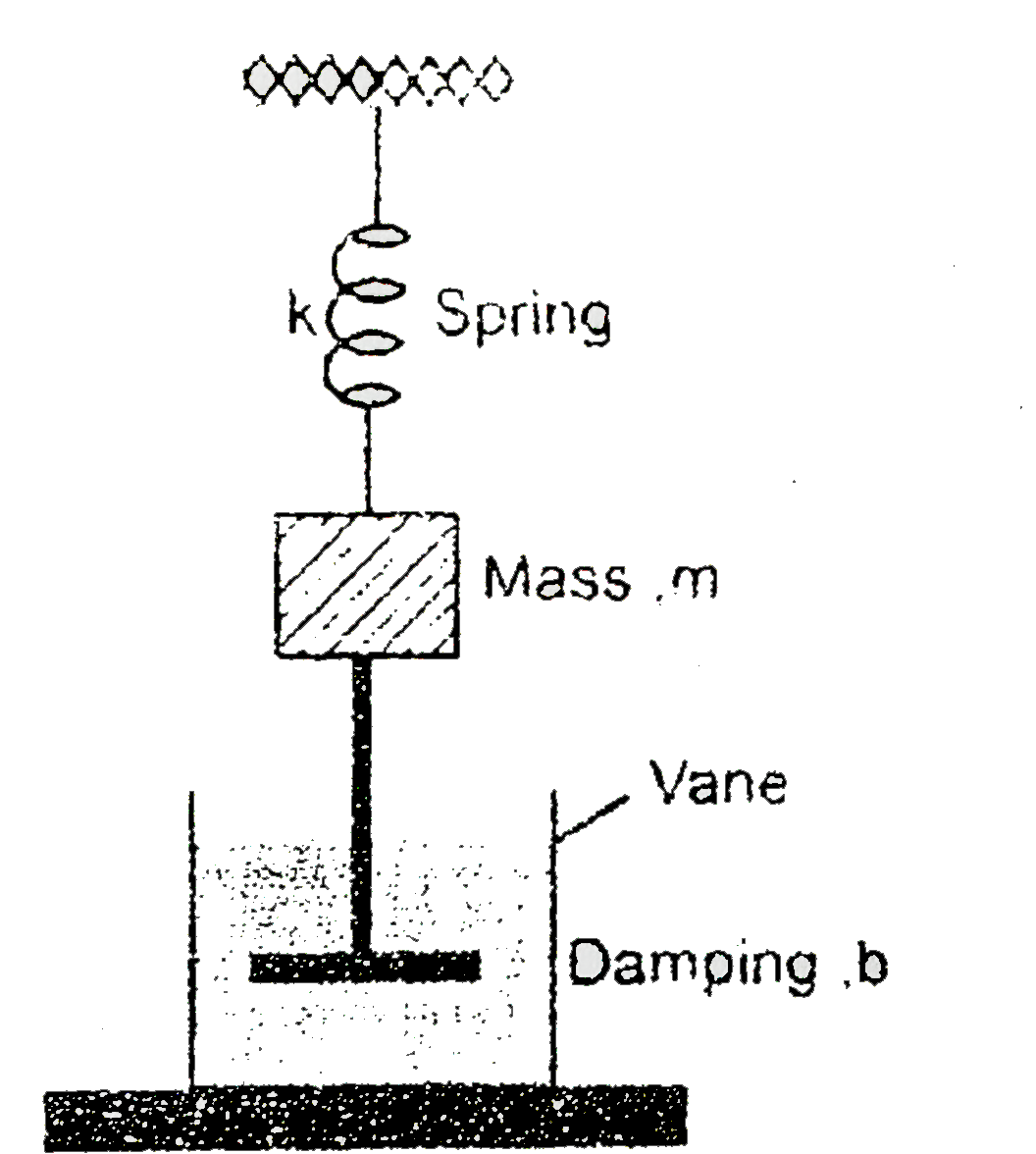
View Solution
Knowledge Check
The displacement of a simple harmonic oscillator is given by x = 4 cos (2πt+π/4)m. Then velocity of the oscillator at t = 2 s is
A4π√2m/sB4π√2m/sC√2π4m/sD4√2πm/sThe position of a simple harmonic oscillator is given by x(t)=(0.50)cos(π3t), where t is measured in seconds. What is the maximum velocity of this oscillator?
A0.17m/sB0.52m/sC0.67m/sD1.0m/sThe displacement of a simple harmonic oscillator is, x = 5 sin (πt/3)m. Then its velocity at t = 1 s, is
Aπ6m/sB5π6m/sC6π6m/sDπ2m/s
For the damped oscillator shown in previous Figure, the mass m of the block is 400 g, k=45Nm−1 and the damping constant b is 80gs−1. Calculate .
(a) The period of osciallation ,
(b) Time taken for its amplitude of vibrations to drop to half of its initial value and
(c ) The time taken for its mechanical energy to drop to half its initial value.
View SolutionIn damped oscillatory motion a block of mass 20kg is suspended to a spring of force constant 90N/m in a medium and damping constant is 40g/s. Find (a) time period of oscillation (b) time taken for amplitude of oscillation to drop to half of its intial value (c) time taken for its mechanical energy to drop to half of its initial value.
View SolutionEquation of motion for a particle performing damped harmonic oscillation is given as x=e−1tcos(10πt+ϕ). The time when amplitude will half of the initial is :
View SolutionThe equation of displacement of a harmonic oscillator is x =3sinωt+4 cosωtamplitude is
View SolutionThe displacement equation of an oscillator is given by x = 5 sin (2πt+0.5π)m. Then its time period and initial displacement are
View Solution
