A uniform sphere of density ρ floats at the interface of two liquids of densities ρ1 and ρ2(>ρ1) The sphere has 23 rd of vertical diameter in denser liquid and remaining part in the other liquid.If aρ=bρ1+cρ2 then b+c-a=_______.
Step by step video & image solution for A uniform sphere of density rho floats at the interface of two liquids of densities rho_(1) and rho_(2)(>rho_(1)) The sphere has (2)/(3) rd of vertical diameter in denser liquid and remaining part in the other liquid.If a rho=b rho_(1)+c rho_(2) then b+c-a=_______. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Equal masses of two substance of densities ρ1andρ2 are mixed together. What is the density of the mixture?
View SolutionA block of density ρ1 floats in two immiscible liquids of density 4ρ and 2ρ , such that (14)th portion is in liquid of density 4ρ and remaining liquid of density 2ρ ,then ρ1=_________g(cm)3(Given ρ=0.8g(cm)3)
View Solution
Knowledge Check
- Question 1 - Select One
A solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
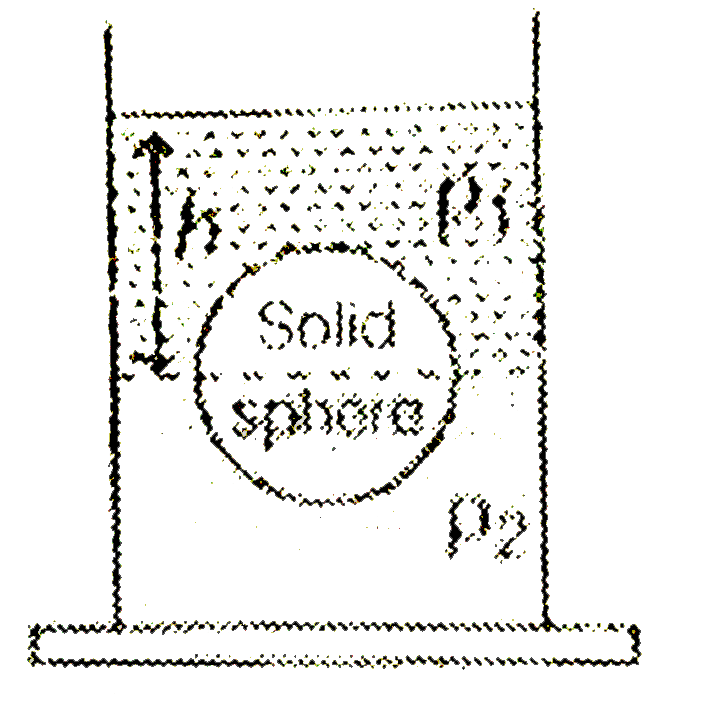 Ap0πr2+(h−23r)πr2ρ1gB(h−23r)πr2ρ1gC23πr2ρ1gDp0×πr2
Ap0πr2+(h−23r)πr2ρ1gB(h−23r)πr2ρ1gC23πr2ρ1gDp0×πr2 - Question 2 - Select One
A solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densityes ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
A(rho-rho_(1))/(rho_(2)-rho)Bρ2−ρρ−ρ1C(rho+rho_(1))/(rho+rho_(2))D(rho+rho_(2))/(rho+rho_(1)) - Question 3 - Select One

A spherical ball of radius R is floating at the interface of two liquids with densities ρ and 2ρ. The volumes of the ball immersed in two liquids are equal. Answer the following questions:
Find the force exerted by the liquid with density 2ρ on the ballAπR2ρg(H+2R3)B23πR2ρgC43πR2ρgD2πR2ρg(H+2R3)
A cube of 1 kg is floating at the interface of two liquids of density ρ1=3/4gm/cm3andρ2=2.5gm/cm3 The cube has (3/5)th part in ρ2 and (2/5)th part in ρ1 .Find the density of the cube .
 View Solution
View SolutionIf two liquids of same masses but densities ρ1andρ2 respectively are mixed, then the density of mixture is given by
View SolutionIf two liquids of same masses but densities ρ1andρ2, respectively are mixed, then the density of mixture is given by
View SolutionA ball of density ρ is released from deep inside of a liquid of density 2ρ. It will move up
View SolutionA narrow U-tube placed on a horizontal surface contains two liquids of densities ρ1 and ρ2 . The columns of the liquids are indicated in the figure. The ratio ρ1ρ2 is equal to :
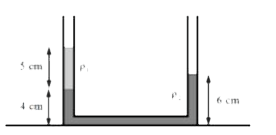 View Solution
View Solution
