काँच (μ=1.5) के एक गोले का व्यास 20 cm है | एक समान्तर बीम इसमें एक ओर से प्रवेश करती है | यह दूसरी ओर कहाँ फोकसित होगी ?
मान लें कि P1 और P2, काँच के गोले के दो पृष्ठ हैं |
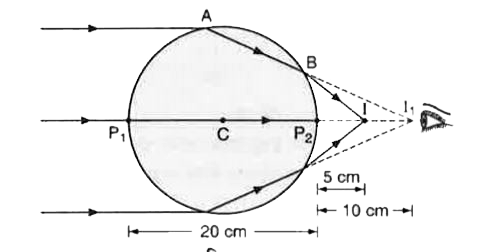
पृष्ठ AP1 पर अपवर्तन : वायु में से आ रही प्रकाश की एक समान्तर बीम, पृष्ठ AP1 पर पड़ती है | अपवर्तन के बाद यह एक बिन्दु I1 पर अभिसरित होगी यदि गोले का पदार्थ सतत हो | इसका अर्थ यह है कि I1, अनन्त पर वस्तु का वास्तविक प्रतिबिम्ब होगा जब अपवर्तन, AP1 पृष्ठ पर हो | यहाँ μ1=1,u=−∞,μ2=1.5 और R=+20/2=+10 cm मान लें कि P1 से प्रतिबिम्ब I1 की दूरी अर्थात P1I1=v1 है |
क्योंकि अपवर्तन, अपेक्षाकृत विरल से अपेक्षाकृत सघन माध्यम में हो रहा है, इसलिए
μ2v−μ1u−μ2−μ1R
या 1.5v1−1−∞=1.5−110=120
या 1.5v1=120
या v1=P1I1=(1.5×20) cm=30 cm
पृष्ठ BP2 पर अपवर्तन : पृष्ठ AP1 पर अपवर्तन के बाद एक बिन्दु I1 पर अभिसरित होने से पहले किरणें, पृष्ठ BP2 से टकराती हैं और अन्त में बिन्दु I पर अभिसरित होती है | यहाँ बिन्दु I1, पृष्ठ BP2 पर अपवर्तन के लिए आभासी वस्तु के रूप में कार्य करता है और I, इसका वास्तविक प्रतिबिम्ब है |
यहाँ u=P2I1=(P1I1−P1P2)=(30−20) cm=+10 cm
और R=−10 cm
मान लें की प्रतिबिम्ब I की P2 से दूरी, v है |
क्योंकि अपवर्तन, अपेक्षाकृत सघन से अपेक्षाकृत विरल माध्यम में हो रहा है, इसलिए
μ1v−μ2u=μ1−μ2R
या 1v−1.510=1−1.510=0.510 या 1v=0.510+1.510=210
या v=5 cm
Topper's Solved these Questions
- गोलीय पृष्ठों और लेन्सों पर अपवर्तन BOOK - GRB PUBLICATION HINDICHAPTER - गोलीय पृष्ठों और लेन्सों पर अपवर्तन EXERCISE - विषय-आधारित समस्याएँ: हल सहित (गोलीय पृष्ठों पर अपवर्तन) विस्थापन विधि
2 Videos
- गोलीय पृष्ठों और लेन्सों पर अपवर्तन BOOK - GRB PUBLICATION HINDICHAPTER - गोलीय पृष्ठों और लेन्सों पर अपवर्तन EXERCISE - विषय-आधारित समस्याएँ: हल सहित (लेन्स और दर्पण का संयोजन)
2 Videos
- गोलीय पृष्ठों और लेन्सों पर अपवर्तन BOOK - GRB PUBLICATION HINDICHAPTER - गोलीय पृष्ठों और लेन्सों पर अपवर्तन EXERCISE - विषय-आधारित अभ्यास (प्रतिरूपी अभ्यास)
21 Videos
- इलेक्ट्रॉनिक युक्तियाँ BOOK - GRB PUBLICATION HINDICHAPTER - इलेक्ट्रॉनिक युक्तियाँ EXERCISE - विषय -आधारित अभ्यास
31 Videos
- चुम्बकत्वBOOK - GRB PUBLICATION HINDICHAPTER - चुम्बकत्वEXERCISE - प्रतियोगिता सामग्री रिक्त स्थान भरना
12 Videos
Similar Questions
एक परदा, वस्तु से 90 cm दूर रखा जाता है | एक उत्तल लेन्स, परदे पर वस्तु का प्रतिबिम्ब, एक दूसरे से 20 cm की दूरी पर दो अलग-अलग स्थानों पर बनाता है | लेन्स की फ़ोकस दूरी निकालें |
View Solutionचित्र 14.36 में दिखाए अनुसार मोमबत्ती, 10 cm फ़ोकस दूरी वाले अवतल दर्पण के वक्रता केन्द्र पर है | अभिसारी लेन्स की फ़ोकस दूरी 32 cm है और यह मोमबत्ती के दाईं ओर 85 cm की दूरी पर है | मोमबत्ती, दाईं ओर से लेन्स में से देखी जाती है | लेन्स, मोमबत्ती के दो प्रतिबिम्ब बनाता है दूसरा प्रतिबिम्ब, उस प्रकाश से बनता है जो मोमबत्ती से दर्पण की ओर जाता है, परावर्तित होता है और फिर लेन्स में से गुज़रता है |
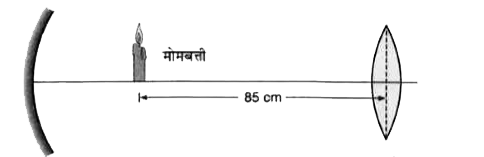
(a) इन दोनों प्रतिबिम्बों के लिए एक मुख्य किरण चित्र बनाएँ जो प्रतिबिम्ब की स्थिति बताए |
(b) हर प्रतिबिम्ब के लिए निम्न प्रश्नों के उत्तर दें :
(i) प्रतिबिम्ब कहाँ है ?
(ii) क्या प्रतिबिम्ब, वास्तविक है या आभासी ?
(iii) या प्रतिबिम्ब, मूल वस्तु के सापेक्ष सीधा है या उलटा ?
View Solution6 cm व्यास और 1.5 अपवर्तनांक वाले गोले में एक छोटा वायु का बुलबुला फँसा है | व्यास के अनुदिश देखने पर बुलबुला, गोले के 1 cm अन्दर प्रतीत होता है | बुलबुले की वास्तविक स्थिति निकालें |
View Solutionएक मादित अर्धचालक में अशुद्धता स्तर, चालन बैंड के 30 MeV नीचे हैं।
(a) क्या पदार्थ , n-प्रकार का है या p-प्रकार का ?
(b) किसी ऊष्मीय टक्कर में ऊर्जा की मात्रा kBT(−30meV), अशुद्धता आयन से शिथिल रूप से बंधे अतिरिक्त इलेक्ट्रान को दी जाती है और यह इलेक्ट्रॉन, चालन बैंड में छलांग लगाने भर के योग्य हो जाता है। ताप T निकालें।
View Solutionएक छड़ चुम्बक को इसकी लम्बाई के लम्बवत दो बराबर टुकड़ों में काटने से एक ही ध्रुव तीव्रता परन्तु.........द्विध्रुव आघूर्ण वाले चुम्बक उत्पन्न होते हैं।
View Solutionबताएं कि एक प्रतिदर्श समष्टि का विभाजन एक है या एक से अधिक?
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionएक धातु के बेलन को, जिसका व्यास 8 से.मी. और ऊँचाई 90 से. मी. है, गलाकर 12 से. मी. व्यास वाले कितने गोले बनाए जा सकते हैं ?
View Solutionयदि गोले का व्यास 14 से. मी. है, तो उसकी त्रिज्या होगी-
View SolutionA regular pyramid has a square base. The height of the pyramid is 22 cm and side of its base is 14 cm. Volume of pyramid is equal to the volume of a sphere. What is the radius (in cm) of the sphere?
एक सम पिरामिड का आधार एक वर्ग है। पिरामिड को ऊँचाई 22 से.मी. है तथा उसके आधार की भुजा 14 से.मी. है। पिरामिड का आयतन एक गोले के आयतन के बराबर हैं गोले की त्रिज्या (से.मी. में) क्या है?
View Solutionभारत में फाइलें एक विभाग से दूसरे विभाग में पहुँचती हैं यह किरा विडम्बना की ओर संकेत करता है?
View Solutionचम्पा कहाँ की एक अनपढ़ बालिका है?
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solutionनिम्नलिखित में से कौन-सा कथन प्राथमिक स्तर पर भाषा सीखने के एक महत्त्वपूर्ण उद्देश्य की ओर संकेत करता है
View Solutionदेवनागरी लिपि के सन्दर्भ में कौन-से कथन सत्य है?
I. देवनागरी में एक ध्वनि के लिए एक ही प्रतीक है।
II. देवनागरी में विदेशी ध्वनियों को व्यक्त करने की क्षमता है।
III. देवनागरी दाई ओर से बाईं ओर लिखी जाती है।
IV. देवनागरी में वर्णों की संख्या रोमन लिपि से कम है।
View Solutionएक ओर अजगरहि लखि एक ओर मृगराय। विकल बटोही बीच ही परयो मूर्छा खाय। उपरोक्त पंक्तियों में प्रयुक्त रस है।
View Solution
