A particle experience an acceleration a=(4e−3t)ms2 along positive x-axis, where t is time in s .If the initial velocity of the particle is 2m/s along positive x-axis,the velocity of the particle when its acceleration becomes zero is?
Step by step video & image solution for A particle experience an acceleration a=(4e^(-3t))m/s^(2) along positive x-axis, where t is time in s .If the initial velocity of the particle is 2m/s along positive x-axis,the velocity of the particle when its acceleration becomes zero is? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
A time varying force, F=2t is acting on a particle of mass 2kg moving along x-axis. velocity of the particle is 4m/s along negative x-axis at time t=0. Find the velocity of the particle at the end of 4s.
View SolutionA particle moves along x-axis with acceleration a=6(t−1) where t is in second. If the particle is initially at the origin and it moves along positive x-axis with v0=2m/s, find the nature of motion of the particle.
View Solution
Knowledge Check
- Question 1 - Select One
. If the velocity of a particle is (10 + 2 t 2) m/s , then the average acceleration of the particle between 2s and 5s is
A2m/s2B4m/s2C12m/s2D14m/s2 - Question 2 - Select One
A particle moves along x-axis and its displacement at any time is given by x(t)=2t3−3t2+4t in SI units. The velocity of the particle when its acceleration is zero is
A2.5ms−1B3.5ms−1C4.5ms−1D8.5ms−1 - Question 3 - Select One
The acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
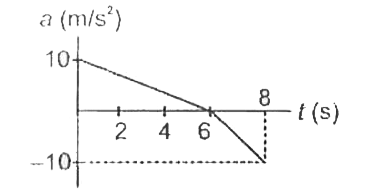 A+15m/sB+20m/sC−15m/sD−20m/s
A+15m/sB+20m/sC−15m/sD−20m/s
If the velocity of a paraticle moving along x-axis is given as v=(4t2+3t=1)m/s then acceleration of the particle at t=1sec is :
View SolutionA particle moves along "x" -axis with an acceleration a=12x2ms−2 .The particle has zero velocity at "x=(-2)m" .Find the velocity of the particle (in m/sec)as it passes through origin.
View SolutionA particle moves along the x-axis obeying the equation x=t(t−1)(t−2), where x is in meter and t is in second
a. Find the initial velocity of the particle.
b. Find the initial acceleration of the particle.
c. Find the time when the displacement of the particle is zero.
d. Find the displacement when the velocity of the particle is zero.
e. Find the acceleration of the particle when its velocity is zero.View SolutionThe motion of a particle along a straight line is described by the equation: x=8+12t−t3, where x is inmeter and t in second.
(i) the initial velocity of particle is 12 m//s
(ii) the retardation of particle when velocity is zero is 12m/s2
(iii) when acceleration is zero, displacement is 8 m
the maximum velocity of particle is 12m/sView SolutionTwo particles are moving along x-axis. Particle-1 is 40m behind Particle-2. Particle-1 starts with velocity12m/s and acceleration 4m/s2 both in positive x-direction. Particle-2 starts with velocity 4m/s and acceleration 12m/s2 also in positive x-direction. Find
(a) the time when distance between them is minimum.
(b) the minimum distacne between them.View Solution
