चित्र में दिखाए गए दो सदिशों A तथा B के बीच का कोण θ है। इनके परिणामी सदिश का परिमाण तथा दिशा उनके परिमाणों तथा θ के पद में निकालिए।
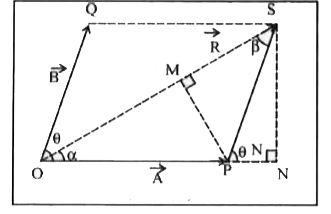
चित्र में सदिश →A व →B को क्रमशः समान्तर चतुर्भुज की आसन्न भुजाओं (adjacent sides) OP तथा OQ द्वारा व्यक्त किया गया है। सदिश →A व →B के मध्य कोण θ है एवं सदिश →A व →B के मध्य कोण α है।
सदिश योग के समान्तर चतुर्भुज नियम से →R=→A+→B
समकोण त्रिभुज ONS से
(OS)=(ON)2+(NS)2
⇒(OS)2=(OP+PN)2+(NS)2
⇒(OS)2=(OP)2+(PN)2+2(OP)(PN)+(NS)2
⇒(OS)2=(OP)2+(PN)2+(NS)2+2(OP)(PN) ...(1)
समकोण त्रिभुज PNS से
(PS)2=(PN)2+(NS)2 .....(2)
cosθ=PNPS
∴PN=PScosθ ..(3)
समी. (1), (2) व (3) से
(OS)2=(OP)2+(PS)2+2(OP)(PScosθ) ...(3)
R2=A2+B2+2(A)(Bcosθ)
⇒R=√A2+B2+2ABcosθ ....(4)
समी. (4) को कोज्या-नियम कहते हैं। समकोण त्रिभुज ONS से
sinα=NSOS=NSR
⇒NS=Rsinα ...(5)
समकोण त्रिभुज PNS से
sinθ=NSPS=NSB
⇒NS=Bsinθ ...(6)
∴ समी. (5) व (6) से
Rsinα=Bsinθ
⇒Rsinθ=Bsinα ...(7)
इसी प्रकार PM=Asinα=Bsinβ
⇒Asinβ=Bsinα ....(8)
समी.(7) व (8) से
Rsinθ=Asinβ=Bsinα ....(9)
समकोण त्रिभुज ONS से
tanα=NSON=NSOP+PN
=BsinθA+Bcosθ
⇒tanα=BsinθA+Bcosθ ...(10)
समी. (9) को ज्या-नियम कहते है।
Topper's Solved these Questions
- समतल में गति BOOK - SCIENCE PUBLICATIONCHAPTER - समतल में गति EXERCISE - TEST YOUR KNOWLEDGE
7 Videos
- समतल में गति BOOK - SCIENCE PUBLICATIONCHAPTER - समतल में गति EXERCISE - MCQ
11 Videos
- मात्रक एवं मापन BOOK - SCIENCE PUBLICATIONCHAPTER - मात्रक एवं मापन EXERCISE - आंकिक प्रश्न
21 Videos
- सरल रेखा में गति BOOK - SCIENCE PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न आंकिक प्रश्न (एक समान त्वरित गति पर आधारित प्रश्न)
19 Videos
Similar Questions
एकांक सदिश से क्या तात्पर्य है?
View Solutionएक बिन्दु पर तीन बल एक साथ लग रहे हैं। दो बलों →F1,F2 क्रमशः (2ˆi−3ˆj) तथा (ˆi−ˆj) है। यदि वस्तु साम्यावस्था में है तो तीसरा बल होगा
View Solutionहवा में ध्वनि का वेग 332 m/s है यदि उसकी लम्बाई को किलोमीटर में तथा समय को घण्टे में नापा जाये तो वेग का नया मान क्या होगा ?
View Solutionएक पिण्ड विरामावस्था से प्रारंभ कर 20मी./से.^2 त्वरण से गति करता है। 6वें सेकण्ड में तय की गई दूरी का मान ज्ञात करो।
View Solutionयदि बिंदु A जिसका स्थिति सदिश ¯a+2¯b है तथा सदिश ¯a,AB को 2:3 के अनुपात में विभाजित करता है तो B का स्थिति सदिश है:
View Solutionयदि ¯u और ¯v एकांक सदिश हों तथा उनके बीच का न्यून कोण θ हो, तो 2¯u×3¯v एक एकांक सदिश होगा :
View Solutionसदिश ¯a=α¯i+2¯j+β¯k, सदिशों ¯b=¯i+¯j तथा ¯c=¯j+¯k के तल में स्थित है तथा ¯b और ¯c के बीच के कोण का समद्विभाजन करता है, तो निम्न में से कौनसा α और β के सम्भावित मान प्रदान करता है ?
View Solutionसदिश →a और →b दो मात्रक सदिश है तथा इनके बीच का कोण α है। यदि →a+→b भी एक मात्रक सदिश है तो α का मान होगा -
View Solutionरेखा x−2a=y−2b=z−2c तथा समतल ax+by+cz+6=0 के बीच का कोण है -
View Solutionसदिश 2ˆi−ˆj तथा ˆi+2ˆj के मध्य का कोण ज्ञात कीजिये।
View Solutionबिंदु P समिष्ट में इस प्रकार है की OP=6 तथा ¯¯¯¯op,OX तथा OY-अक्षो के साथ क्रमश: 45∘ व 60∘ के कोण बनता है तो का स्थिति सदिश होगा -
View Solutionसदिश →a=ˆi+ˆj+ˆk का सदिशों →b=2ˆi+4ˆj−5ˆk तथा →c=λˆi+2ˆj+3ˆk के योगफल की दशा में एक मात्रक सदिश के साथ अदिश गुणनफल 1 के बराबर है का मान ज्ञात कीजिए तथा →b+→c की दशा में एक मात्रक सदिश ज्ञात कीजिए।
View Solutionयदि →a=ˆi+2ˆj+2ˆk,∣∣→b∣∣=5 और →a तथा→b के बीच कोण π6 है , तब दोनों भुजाओं के रूप में इन दो सदिशों के द्वारा बनने वाले त्रिभुज का क्षेत्रफल है -
View Solutionकोई रेखा x-अक्ष और y-से साथ क्रमशः 60∘ तथा 45∘ के कोण बनाती है। इनके द्वारा घनत्व दिशा में z-अक्ष के साथ कितना कोण बनेगा ?
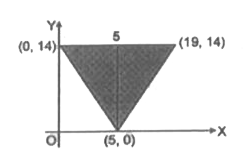
View Solutionचित्र में दिखाए गए छायांकित क्षेत्र के लिए असामिका है-
View Solutionयदि α=(λ−2)a+b तथा β=(4λ−2)a+3b दो दिए गए सदिश है, जहाँ सदिश a तथा b सरीख नहीं है । λ का वह मान जिसके लिए α तथा β सरीख है, है
View Solution
