The radius of a circle with centre at origin is 30 units. Write the coordinates of the points where the circle intersects the axes. Find the distance between any two such points. Solution in Tamil
Step by step video & image solution for The radius of a circle with centre at origin is 30 units. Write the coordinates of the points where the circle intersects the axes. Find the distance between any two such points. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COORDINATE GEOMETRYBOOK - FULL MARKSCHAPTER - COORDINATE GEOMETRYEXERCISE - EXERCISE -5.3
7 Videos
- COORDINATE GEOMETRYBOOK - FULL MARKSCHAPTER - COORDINATE GEOMETRYEXERCISE - EXERCISE -5.4
7 Videos
- COORDINATE GEOMETRYBOOK - FULL MARKSCHAPTER - COORDINATE GEOMETRYEXERCISE - EXERCISE -5.1
4 Videos
- ALGEBRA BOOK - FULL MARKSCHAPTER - ALGEBRA EXERCISE - Assignment Answer the following questions :
1 Videos
- GEOMETRYBOOK - FULL MARKSCHAPTER - GEOMETRYEXERCISE - Assignment (IV. Answer the following questions)
9 Videos
Similar Questions
The centre of a cirlce is (-4,2) . If one end of the diameter of the circle is (-3,7) tehn find the other end.
View SolutionFind the coordinate of the point of the point which divides the line segment joining the points A(4,-3) and B(9,7) in the ratio 3:2.
View SolutionPlot the following points in the coordinate system and identify the quadrants P(−7,6),Q(7,−2),R(−6,−7)S(3,5)andT(3,9).
View SolutionSubtract 5x2−4y2+6y−3 from 7x2−4xy+5y2+5x−3y
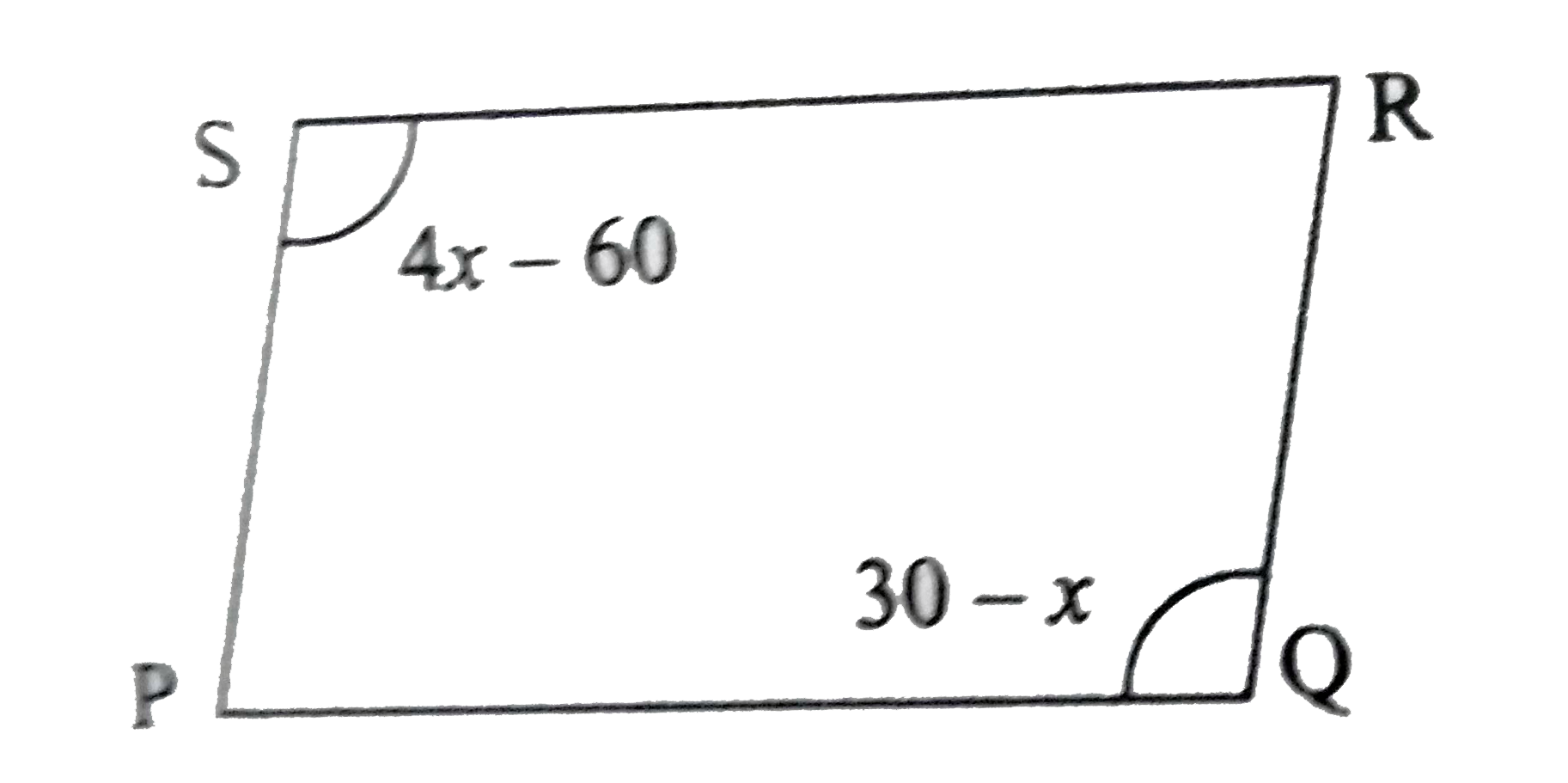
View SolutionIn the given diagram PQRS is a parellelogram.
∠S=4x−60∠Q=30−x. Find the angles of P and R .
View SolutionTwo circles of radil 5cm and 3cm intersect at two points and the distance between their centres is 4cm. Find the length of the common chord.
View SolutionTwo circles of radii 5 cm and 3cm intersect at two points and the distance between their centres is 4cm. Find the length of the common chord.
Let the common chord be AB and Pand Q be the centers of the two circles.
AP=5cmand AQ=3cm.
PQ=4cm ...given
Now, segPQ⊥chordAB
AR=RB=12AB....perpendicular from center to the chord, bisects the chord
Let PR=xcm
so RQ=(4−x)cm
In△ARP,AP2=AR2+PR2
AR2=52−x2...(1)
In △ARQ,AQ2=AR2+QR2
AR2=32−(4−x)2...(2)
52−x2=32−(4−x)2...from (1) & (2)
25−x2=9−(16−8x+x2)
25−x2=−7+8x−x2
32=8x
x=4 substituting in equation(1) we get , AR2=25−16=9
AR=3cm
AB=2×AR=2×3=6
AB=6cmSo length of common chord is6 cm.
View SolutionThe locus of the centre of the circle passing through the origin O and the points of intersection A and B of any line through (a, b) and the coordinate axes is
View SolutionTwo circles are intersect externally if radius of one circle is 3.5 cm and other is 6.5 cm find the distance between their centres.
View Solutiona अर्धव्यास वाले वृत्त पर चार बिंदु A,B,C,D अक्षों पर हैं तथा वृत्त का केंद्र मूल बिंदु O है तो चारों बिंदुओं के निर्देशांक ज्ञात कीजिए।
View SolutionThe radius of a circle with centre at origin is 30 units. Write the coordinates of the points where the circle intersects the axes. Find the distance between any two such points.
View SolutionFind the equation of circle passing through intersection points of line ax+by+c=0 with coordinate axes and through origin.
View SolutionTwo circles of equal radius of 5 units have their centres at the origin and the point (2,−3). Equation of the common chord of these circles is
View SolutionFind the equation of circle passing through intersection points of line ax+by+c=0 with coordinate axes and through origin.
View SolutionFind the equation of circle passing through intersection points of line ax+by+c=0 with coordinate axes and through origin.
View Solution
