गॉस के नियम को लिखें। इसकी सहायता से किसी अनन्त विस्तारित समरूप आवेशित पतले आवेशित सीधे तार के कारण किसी बिन्दु पर विद्युत क्षेत्र की तीव्रता के लिए व्यंजक प्राप्त करें।
गॉस का प्रमेय - गॉस प्रमेय कार्ल गॉस के द्वारा दिया गया था। इस प्रमेय द्वारा किसी किसी विद्युत क्षेत्र में रखे गए किसी बंद तल से होकर गुजरने वाले कुल विद्युत फ्लक्स एवं तल के अंदर स्थित कुल आवेश में संबंध ज्ञात होता है।
कथन - विद्युत क्षेत्र में किसी बंद तल से होकर गुजरने वाला विद्युत फ्लक्स तल से होकर गुजरने वाला कुल विद्युत फ्लक्स तल के भीतर उपस्थित कुल विद्युत आवेश का 1ε0 गुणा होता है जहाँ ε0 मुक्त आकाश की परावैधुता है।
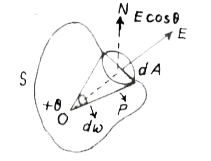
अर्थात ϕE=∮→E.−→dA=1ε0h∑i=lθ
अनंत लम्बाई के आवेशित तार के कारण विद्युत क्षेत्र की तीव्रता - माना कि AB एक अनंत लम्बाई तथा एक समान रूप से आवेशित चालाक है। जिसके प्रति एकाक लम्बाई पर आवेश λ है। जैसा कि नीचे चित्र में दिखाया गया है।
बेलन के अक्ष से r दूरी पर कोई बिन्दु P स्थित है। जहाँ आवेशित बेलन के कारण विद्युत क्षेत्र की तीव्रता E ज्ञात करनी है।
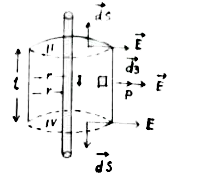
अब जैसा कि चित्र में दिखाया गया है आवेशित बेलन के समाक्षीय ,l लम्बाई तथा r त्रिज्या के एक दूसरे बेलनाकार तथा CD को कल्पना करें जो P से होकर गुजरता है। इसके समतल सिरे अक्ष के लंबवत है। ऐसी सतह गॉसीयन समतल कहा जाता है।
चूँकि बेलन की वक्र सतह का क्षेत्रफल 2πrl
अतः इसके संपूर्ण तल से गुजरने वाले फ्लक्स =ϕE=EA=E2πrl
गॉसीयन सतह तीन भाग में बाटा जा सकता है। भाग (i),(ii) और (iii) में जैसा कि चित्र में दिखाया गया है।
अब ∮→E.→ds=1ε0θ
अतः ∫I→E.→ds+∫II→E.→ds±∫III→E.→ds=1Σ0λl [चूँकि θ=λl]
या ∫Edscosθ+∫Edscosθ+∫Edscosθ=λlε0
चूँकि समतल (i) के लिए θ=0∘
समतल (ii) के लिए θ=90∘
समतल (iii) के लिए θ=90∘
अतः E∫ds+0+0=λlΣ0or,E×2πrh=1ε0λh.
E=12πε0λrE=12πε02λr .
Topper's Solved these Questions
- भौतिक विज्ञान -2009BOOK - BIHAR BOARD- PREVIOUS YEAR PAPERCHAPTER - भौतिक विज्ञान -2009EXERCISE - खण्ड-II (गैर-वस्तुनिष्ट प्रश्न )(लघु उत्तरीय प्रश्न )
11 Videos
- भौतिक विज्ञान - 2013BOOK - BIHAR BOARD- PREVIOUS YEAR PAPERCHAPTER - भौतिक विज्ञान - 2013EXERCISE - खण्ड-II (दीर्घ उत्तरीय प्रश्न )
8 Videos
- भौतिक विज्ञान 2012BOOK - BIHAR BOARD- PREVIOUS YEAR PAPERCHAPTER - भौतिक विज्ञान 2012EXERCISE - खंड-II (गैर-वस्तुनिष्ठ)
19 Videos
Similar Questions
प्रतिरोधकता क्या है ? इसका SI मात्रक लिखें। किसी प्ररूपी अर्धचालक के लिए तापमान में परिवर्तन के साथ प्रतिरोधकता के बदलाव को ग्राफ द्वारा प्रदर्शित करें।
View Solutionहाइगन के तरंग सिद्धांत के आधार पर परावर्तन के नियमों को सिद्ध कीजिए ।
View Solutionक्रांतिक कोण को परिभाषित करें तथा इसकी शर्तो को लिखे।
View Solutionअनंत लंबाई के एकसमान आवेशित सीधे तार के कारण विद्युत क्षेत्र || कुछ प्रश्न
View Solutionअनंत लंबाई के एकसमान आवेशित सीधे तार के कारण विद्युत क्षेत्र || कुछ प्रश्न
View Solutionएकसमान आवेशित पतले गोलीय खोल के कारण विद्युत क्षेत्र || कुछ प्रश्न
View Solutionविद्युत क्षेत्र आवेशित गोले के कारण || कुछ प्रश्न
View Solutionआवेशित वलय के कारण विद्युत क्षेत्र की तीव्रता
View Solutionअनंत लंबाई के एकसमान आवेशित सीधे तार के कारण विद्युत क्षेत्र
View Solutionएकसमान आवेशित अनंत समतल चादर के कारण विद्युत क्षेत्र
View Solutionआवेशित वलय के कारण उसकी अक्ष पर विद्युत क्षेत्र
View Solutionसमरूप आवेशित अनंत आकार की चालाक एवं कुचालक पट्टिका के कारण विद्युत क्षेत्र
View Solutionसमरूप आवेशित वलय के कारण उसकी अक्ष पर विद्युत क्षेत्र
View Solutionसीधे धारावाही चालक तार के कारण किसी बिन्दु पर चुंबकिय क्षेत्र की तीव्रता
View Solutionअनंत लंबाई के एकसमान आवेशित सीधे के कारण विद्युत क्षेत्र |एकसमान आवेशित अनंत समतल चादर के कारण विद्युत क्षेत्र |प्रश्न |OMR|Summary
View Solutionआवेशित वलय के कारण विद्युत क्षेत्र
View Solution
