∣∣→A×→B∣∣2+∣∣→A.→B∣∣2का मान ज्ञात कीजिए।
A2B2
Topper's Solved these Questions
- BOOK - SCIENCE PUBLICATIONCHAPTER - कणों के निकाय तथा घूर्णी गति EXERCISE - बोधात्मक प्रश्न16videos
कणों के निकाय तथा घूर्णी गति
- BOOK - SCIENCE PUBLICATIONCHAPTER - कणों के निकाय तथा घूर्णी गति EXERCISE - NCERT TEXT BOOK PROBLEMS21videos
कणों के निकाय तथा घूर्णी गति
- BOOK - SCIENCE PUBLICATIONCHAPTER - कणों के निकाय तथा घूर्णी गति EXERCISE - MCQs11videos
कणों के निकाय तथा घूर्णी गति
- BOOK - SCIENCE PUBLICATIONCHAPTER - उष्मागतिकीEXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न)28videos
उष्मागतिकी
- BOOK - SCIENCE PUBLICATIONCHAPTER - कार्य, ऊर्जा एवं शक्ति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकित प्रश्न ) टक्करों पर आधारित प्रश्न8videos
कार्य, ऊर्जा एवं शक्ति
Similar Questions
किसी भी पिण्ड का जड़त्व आघूर्ण का मान किसी अक्ष के परितः कब न्यूनतम होता है?
01:40View Solutionएकसमान द्रव्यमान घनत्व के निम्नलिखित पिण्डों में प्रत्येक के द्रव्यमान केंद्र की अवस्थिति लिखिए
(a) गोला, (b) सिलिंडर, (c) छल्ला तथा (d) घन।
क्या किसी पिण्ड का द्रव्यमान केंद्र आवश्यक रूप से उस पिण्ड के भीतर स्थित होता हैं?01:42View Solutionयदि HCI अणु में H' की द्रव्यमान-केन्द्र से दूरी x हो तो CI35 की दूरी होगी
02:47View Solutionएक निकाय का P-V आरेख जो कि ऊष्मागतिकी परिवर्तन प्रदर्शित करता है। चित्र में दर्शाया गया है। निकाय पर किया गया कार्य A→B→C 50J है ,आंतरिक ऊर्जा में परिवर्तन ज्ञात कीजिये,दी गई ऊष्मा 84 J है।
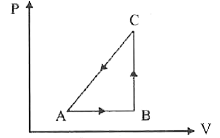 02:47View Solution
02:47View Solutionदो किलोग्राम द्रव्यमान का एक पिण्ड किसी अन्य स्थिर पिण्ड से पूर्णतः अप्रत्यास्थ टक्कर करता है। यदि टक्कर के बाद दोनों पिण्ड उसी दिशा में पहले पिण्ड की एक चौथाई चाल से गतिमान हो तो दुसरे पिण्ड का द्रव्यमान ज्ञात करिये।
09:34View SolutionIf →aand→b are two vectors, such that ∣∣→a×→b∣∣=2 , then find the value of [→a→b→a×→b]
02:07View SolutionIf →aand→b are two vectors, such that ∣∣→a×→b∣∣=2 , then find the value of [→a→b→a×→b]
02:53View SolutionProve that ∣∣→a×→b∣∣2=∣∣∣→a⋅→a→a⋅→b→a⋅→b→b⋅→b∣∣∣.
02:12View Solutionसदिशों तथा के लिए सिद्ध कीजिए कि
∣∣→a×→b∣∣2=∣∣∣→a.→a→a.→b→a.→b→a.→b∣∣∣03:24View Solutionसिद्ध कीजिए :
(i) (→A+→B)−(→A−→B)2=4(→A⋅→B).
(ii) (→A+→B)×(→A−→B)=−2(→A×→B).
(iii) (→A×→B)2+(→A⋅→B)2=A2B2.01:20View Solutionदर्शाइए कि (→a−→b)×(→a+→b)=2(→a×→b)
02:52View Solution→a और →b असंरेख है |यदि सदिश →α=(x−2)→a+→b और →β=(3+2x)→a−2→b संरेख सदिश हो तो x का मान ज्ञात कीजिए|
01:18View Solutionयदि →a और →b असंरेख है ,तो x का मान ज्ञात कीजिए| जिसके लिए सदिश α=(2x+1)→a−→b और β=(x−2)→a+→b संरेख है
03:06View Solutionयदि →a+→b+→c=0 तो सिद्ध कीजिए कि →a×→b=→b×→c=→c×→a इस परिमाण का ज्यामितीय विमोचन कीजिए |
03:11View Solutionপ্রমাণ করাে যে, (→a–→b)×(→a+→b)=2(→a×→b)
00:45View SolutionIf →aand→b are two vectors, such that ∣∣→a×→b∣∣=2 , then find the value of [→a→b→a]×→b .
03:27View Solution

