A particle of mass m is connected with a string of length 2 meter. Other end of the string is fixed with a point O at a height 1 m above the ground. The particle is thrown from some point in such a way that it strikes the ground (perfectly inelastic) with velocity v0 at an angle 37∘ with vertical just below O.

P-2, Q-3, R-1, S-4
P-3, Q-2, R-4, S-1
P-4, Q-1, R-2, S-3
P-2, Q-3, R-4, S-1
The correct Answer is:C
(A) as the collision is perfectly inelastic, velocity after collision is v0sin37∘=35v0 towards right till string becomes taut.
R=v2a⊥=v20gsin37∘=5v203g
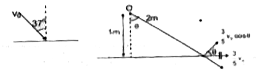
(B) from figure, cosθ=12⇒θ=60∘
after string becomes taut particle motion will seize along the string due to impulse. Just after impulse velocity of particle is 35v0cosθ=310v0 perpendicular to the string from conservation of mechanical energy , 12m(310v0)2=12m(√2g)2+2mg(1+cos60) simplifying, v0=20√2g3m/s
(C ) WG=−2mg(1+cos60∘)=−3mg
∴−WG=3mg
(D) At highest point velocity will be perpendicular to gravitational force
∴P=→F→V=0
Topper's Solved these Questions
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - Exercise
20 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (Short Answer Type Questions)
2 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - SOLVED PROBLEMS (OBJECTIVE) NUMERICAL BASED QUESTIONS
3 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSERTION REASONING TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -4
3 Videos
Similar Questions
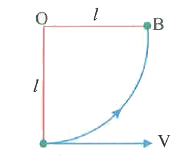
A particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
View SolutionA uniform rod of mass m and length 2L on a smooth horizontal surface. A particle of mass m is connected to a string of length L whose other end is connected to the end ‘A’ of the rod. Initially the string is held taut perpendicular to the rod and the particle is given a velocity v0 parallel to the initial position of the rod.
(a) Calculate the acceleration of the centre of the rod immediately after the particle is projected.
(b) The particle strikes the centre of the rod and sticks to it. Calculate the angular speed of the rod after this.

View Solution
Knowledge Check
A particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
AThe string becomes slack when the partice reaches its highest pointBThe velocity of the particle becomes zero at the highest point.CThe kinetic energy of the ball in initial position was 12mv2=mgDThe particle again passes through the initial position.A particle of mass m is suspended from a string of length l fixed to the point O. What velocity should be imparted to the particle in its lowermost position so that the string is just able to reach the horizontal diameter of the circle?
 Av=√2glBv=√3glCv=√glDv=2gl
Av=√2glBv=√3glCv=√glDv=2glA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl

The maximum angle made by the string with downward vertical isAcos−1(14)Bsin−1(14)Cπ2+cos−1(14)Dπ−cos−1(14)
A particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl

The maximum angle made by the string with downward vertical is
View SolutionA particle of mass 1kg is attached to a string of length 5m. The string is attached to a fixed point O. It is released from the position as shown in Fig. Calculate
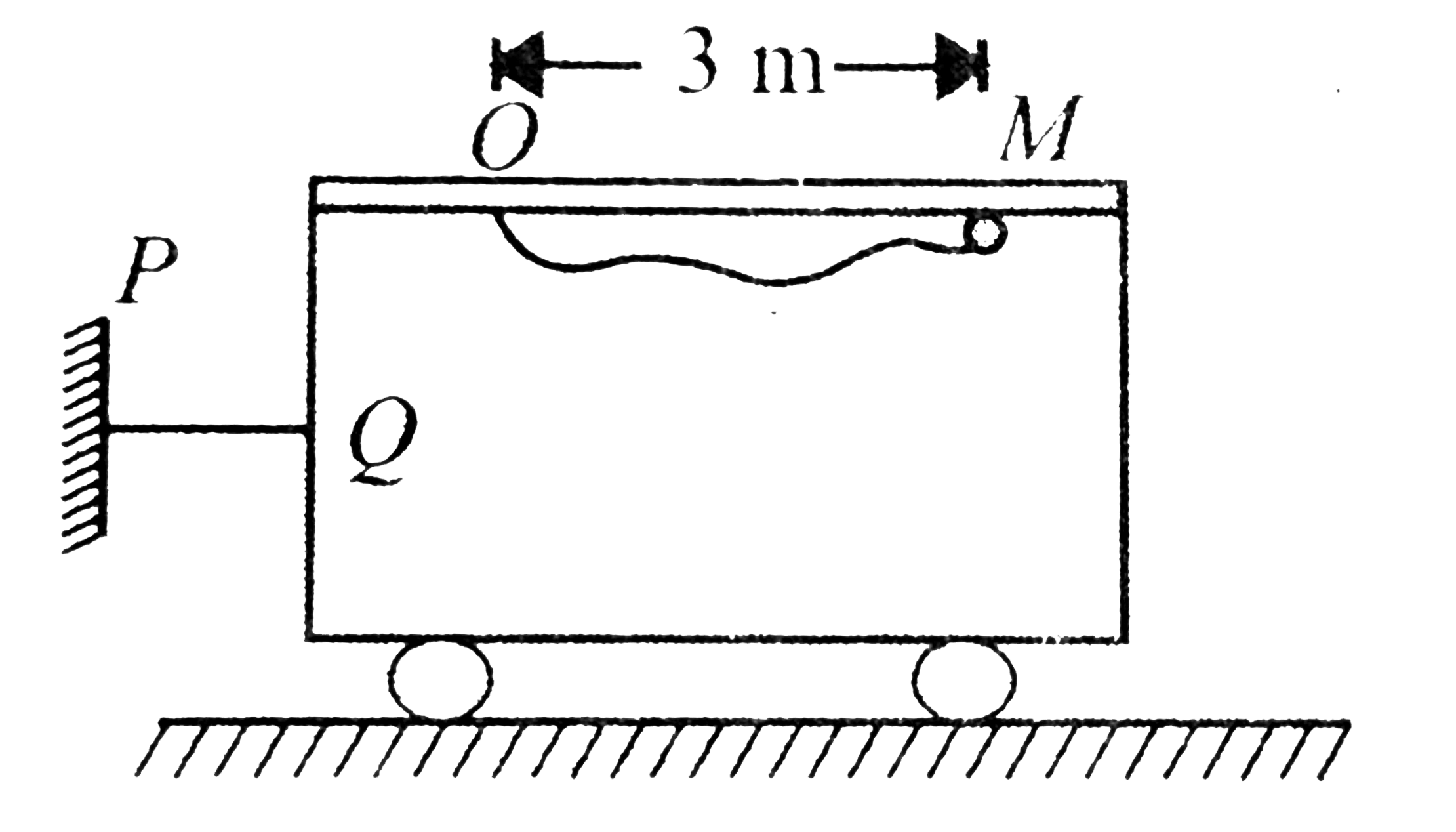
a. the impulse developed in the string when it becomes taut,
b. the velocity of the particle just after the string becomes taut,
c. the impulse developed in this string PQ at this instant.
View SolutionA particle of mass 1kg is attached to a string of length 5m. The string is attached to a fixed point O. It is released from theposition as shown in Fig. Calculate

a. the impulse developed in the string when it becorries taut,
b. the velocity of the particle just after the string becomes taut,
c. the impulse developed in this string PQ at this instant.
View SolutionA particle of mass 'm' is projected from ground with velocity u making angle θ with the vertical. The de-Broglie wave length of the particle at the highest point is:
View SolutionIn a conical pendulum arrangement, a string of length 1 m is fixed at one end with a bob of mass 100g and the string makes 4radpersec around a vertical axis through a fixed point. The angle of inclination of the string with vertical is: (Take g=10ms−1)
View Solution
