A hemispherical open bowl of radius R is placed on a smooth floor. A massive ball falls from some height and collides on the circumference of the bowl. Considering contact point of the floor as origin, position vector of the initial contact point of the bowl when the bowl turns 90∘ will be :
−R2ˆi+Rˆj
−R3ˆi+Rˆj
−R4ˆi+Rˆj
−Rˆi+Rˆj
The correct Answer is:A
Topper's Solved these Questions
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - I (ASSERTION REASONING TYPE)
2 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - II
20 Videos
- COLLISION BOOK - FIITJEECHAPTER - COLLISION EXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - II
17 Videos
- AC CIRCUITSBOOK - FIITJEECHAPTER - AC CIRCUITSEXERCISE - ASSERTION REASONING TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -4
3 Videos
Similar Questions
A hollow hemispherical bowl of mass m radius R is placed on a smooth horizontal surface. A particle (also of mass m) strikes the hemi spherical bowl at point P and sticks to it. the velocity of particle just after the collision in vertically upwards direction is ku25, where k is an integer. Find k.

View SolutionA particle of mass m is released in a smooth hemispherical bowl from shown position A. Find work done by gravity as it reaches the lowest point B.
View Solution
Knowledge Check
A small ball is pushed from a height h along a smooth hemispherical bowl of rodius R. With what speed should the ball be pushed so that it just reaches the top of the opposite end of the bowl?
A√2ghB√2g(R+h)C√2g(R−h)DNone of these
A particle of mass m is released in a smooth hemispherical bowl from shown position A. Find work done by gravity as it reaches the lowest point B.
View SolutionA particle of mass m is released in a smooth hemispherical bowl from shown position A. Find work done by gravity as it reaches the lowest point B.
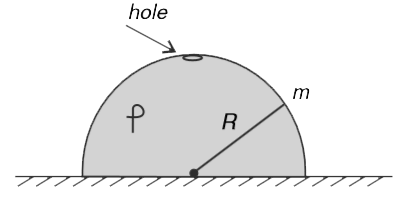
View SolutionA hemispherical bowl of radius R is placed upside down on a flat horizontal surface. There is a small hole at the top of the inverted bowl. Through the hole, a liquid of density ρ is poured in. Exactly when the container gets full, water starts leaking from between the table and the edge of the container. Find the mass (m) of the contaienr.
View SolutionA hemispherical bowl of radius R is rotating about its own axis (which is vertical) with an angular velocity ω . A particle on the frictionless inner surface of the bowl is also rotating with the same ω . The particle is a height h from the bottom of the bowl.
(i) Obtain the relation between h and ω _________
(ii) Find minimum value of ω needed, in order to have a non-zero value of h _____________ .
View SolutionA hemispherical bowl of radius R is rotating about its own axis (which is vertical) with an angular velocity ω . A particle on the frictionless inner surface of the bowl is also rotating with the same ω . The particle is a height h from the bottom of the bowl.
(i) Obtain the relation between h and ω _________
(ii) Find minimum value of ω needed, in order to have a non-zero value of h _____________ .
View SolutionA small ball is pushed from a height h along a smooth hemispherical bowl of radius R. With what speed should the ball be pushed so that it just reaches the top of the opposite end of the bowl?
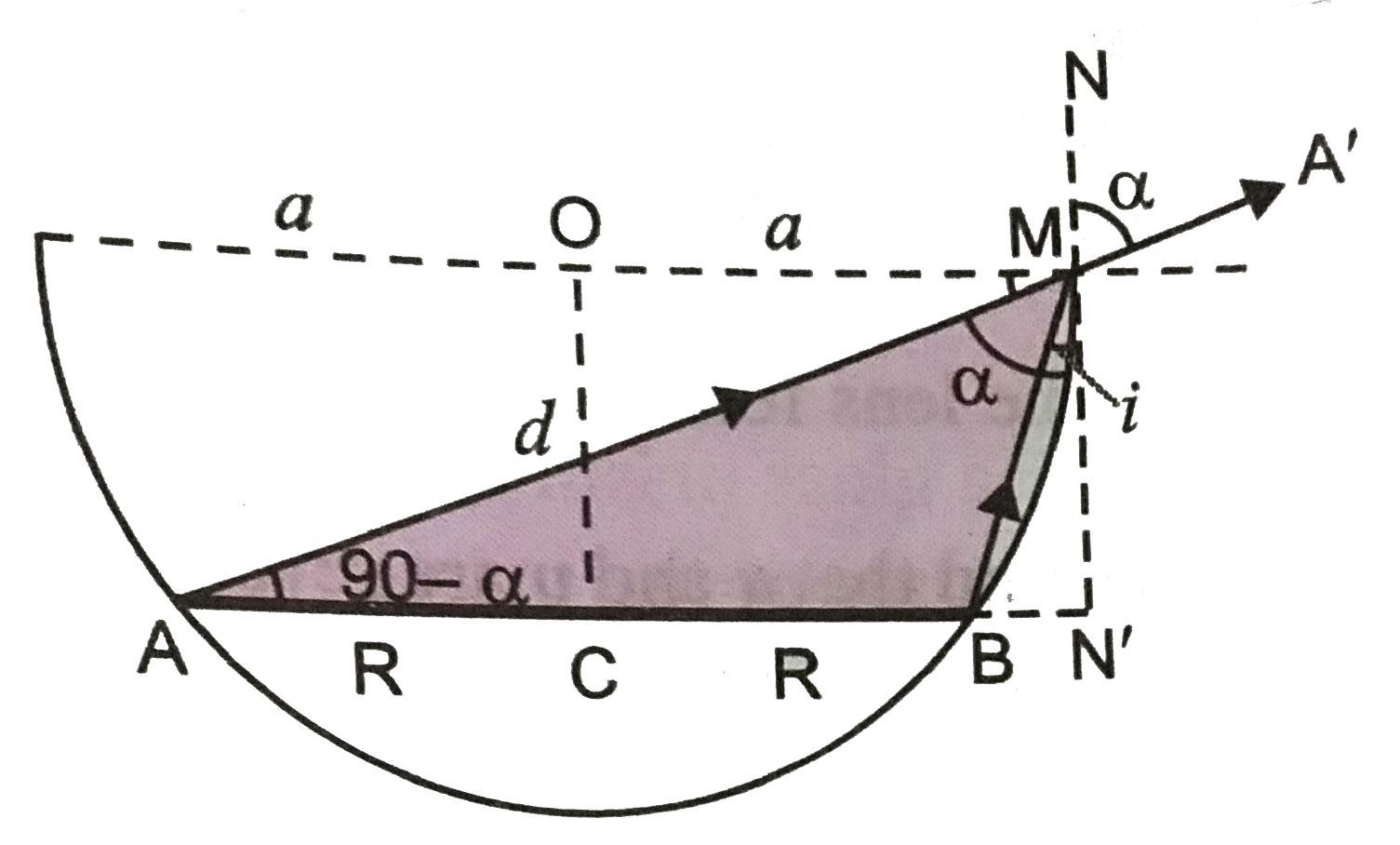
View SolutionA circular disc of radius 'R' is placed co-axially and horizontally inside and opaque hemispherical bowl of radius 'a', Fig. The far edge of the disc is just visible when viewed from the edge of the bowl. The bowl is filled with transparent liquid of refractive index μ and the near edge of the dise becomes just visible. How far below the top of the bowl is the disc placed ?
 .
.
View Solution
