A ball is projected from the floor of a cabin of height 7m with speed 20 m/s at an angle of 37∘ with the floor of cabin. It makes a successive collision with the wall of cabin and then return again to its floor. Assume all collisions are perfectly elastic. Find time taken (in sec) by the ball to reach the floor after collisions with the ceiling of cabin.
The correct Answer is:1
To solve the problem step-by-step, we will analyze the motion of the ball after it is projected, calculate the time taken to reach the ceiling, and then determine the time taken to return to the floor after the collision with the ceiling.
Step 1: Break down the initial velocity into components
The ball is projected with a speed u=20m/s at an angle θ=37∘ with the horizontal. We can find the horizontal and vertical components of the initial velocity:
- Horizontal component ux=ucos(θ)=20cos(37∘)
- Vertical component uy=usin(θ)=20sin(37∘)
Using cos(37∘)≈0.8 and sin(37∘)≈0.6:
- ux=20×0.8=16m/s
- uy=20×0.6=12m/s
Step 2: Calculate the time taken to reach the ceiling
The height of the cabin is h=7m. We can use the kinematic equation for vertical motion to find the time t1 taken to reach the ceiling:
h=uyt1−12gt21
Where g=10m/s2. Plugging in the values:
7=12t1−12⋅10⋅t21
This simplifies to:
7=12t1−5t21
Rearranging gives:
5t21−12t1+7=0
Step 3: Solve the quadratic equation
Now we can use the quadratic formula t=−b±√b2−4ac2a:
Here, a=5,b=−12,c=7:
t1=12±√(−12)2−4⋅5⋅72⋅5
t1=12±√144−14010
t1=12±√410
t1=12±210
Calculating the two possible values:
1. t1=1410=1.4s
2. t1=1010=1.0s
Since the ball will reach the ceiling first, we take t1=1.4s.
Step 4: Calculate the velocity just before the collision with the ceiling
Using the vertical motion equation:
vy=uy−gt1
vy=12−10⋅1.4=12−14=−2m/s
The negative sign indicates that the ball is moving downward just before the collision.
Step 5: Determine the velocity after the elastic collision
In a perfectly elastic collision, the ball will rebound with the same speed but in the opposite direction. Thus, the velocity after the collision is:
vy,after=2m/s(upward)
Step 6: Calculate the time taken to reach the floor after the collision
Now we need to find the time t2 it takes to fall from the ceiling back to the floor. Using the kinematic equation again:
s=vy,aftert2+12gt22
7=2t2+12⋅10t22
7=2t2+5t22
Rearranging gives:
5t22+2t2−7=0
Step 7: Solve the quadratic equation for t2
Using the quadratic formula again:
t2=−2±√(2)2−4⋅5⋅(−7)2⋅5
t2=−2±√4+14010
t2=−2±√14410
t2=−2±1210
Calculating the two possible values:
1. t2=1010=1.0s
2. t2=−1410 (not possible since time cannot be negative)
Thus, the time taken by the ball to reach the floor after the collision with the ceiling is:
t2=1.0s
Final Answer
The total time taken by the ball to reach the floor after the collision with the ceiling is 1.0s.
---
The ball is projected with a speed u=20m/s at an angle θ=37∘ with the horizontal. We can find the horizontal and vertical components of the initial velocity:
- Vertical component uy=usin(θ)=20sin(37∘)
- ux=20×0.8=16m/s
- uy=20×0.6=12m/s
The height of the cabin is h=7m. We can use the kinematic equation for vertical motion to find the time t1 taken to reach the ceiling:
Now we can use the quadratic formula t=−b±√b2−4ac2a:
t1=12±√144−14010
t1=12±√410
t1=12±210
2. t1=1010=1.0s
Using the vertical motion equation:
vy=12−10⋅1.4=12−14=−2m/s
In a perfectly elastic collision, the ball will rebound with the same speed but in the opposite direction. Thus, the velocity after the collision is:
Now we need to find the time t2 it takes to fall from the ceiling back to the floor. Using the kinematic equation again:
7=2t2+12⋅10t22
7=2t2+5t22
Using the quadratic formula again:
t2=−2±√4+14010
t2=−2±√14410
t2=−2±1210
2. t2=−1410 (not possible since time cannot be negative)
The total time taken by the ball to reach the floor after the collision with the ceiling is 1.0s.
Topper's Solved these Questions
Similar Questions
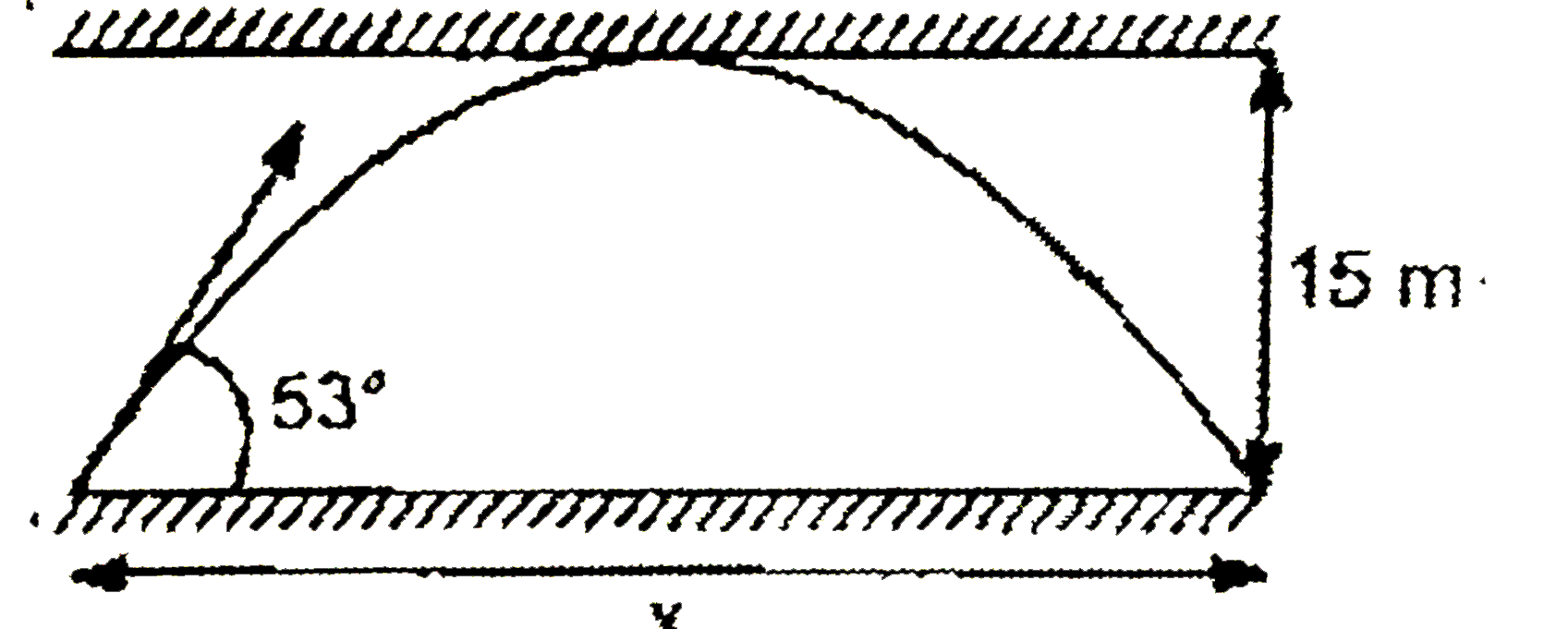
A ball is shot in a long hall having a roof at a height of 15 cm with speed of 25 m/s at angle of 53∘ with the floor. The ball lands on the floor at a distance shown x=____ m form the point of projection .
 View Solution
View SolutionA ball strikes an identical ball with velocity 50 m/s and after the collision which is perfectly elastic it is found to move with velocity 30 m/s . Show that the two balls move at right angles to each other after collision .
View Solution
Knowledge Check
- Question 1 - Select One
A particle is projected from a horizontal floor with speed 10m/s at an angle 30∘ with the floor and striking the floor after sometime. State which is correct.
Avelocity of particle will be perpendicular to initial direction two seconds after projection.Bminimum speed of particle will be 5m/sec.CDisplacement of particle after half second will be 35/4m.DNone of these - Question 2 - Select One or More
A particle is projected from a horizontal floor with speed 10ms at an angle 30∘ with the floor and striking the floor after sometime. State which is correct.
AVelocity of particle will be perpendicular to initial direction two seconds after projection.BMinimum speed of particle will be 5√3msec.CDisplacement of particle after half second will be 14√235mDThe particle will strike the floor at 2 sec. - Question 3 - Select One
A ball is shot in a long hall having a roof at a height of 10m with 25m/s at an angle of 37∘ with the floor. The ball lands on the floor at a distance of ………………….. from the point of projection. ( Assume elastic collisions if any )
 A40mB60mC45/4mD20m
A40mB60mC45/4mD20m
A massive vertical wall is approaching a man at a speed μ. When it is at a distance of 10m, the man throws a ball with speed 10 m/s at an angle of 37∘, which after having a completely elastic collision with the wall, reaches back directly into the hands of the man. The velocity of the wall is
View SolutionA ball is projected from ground with a velocity V at an angle θ to the vertical. On its path it makes an elastic collision with a vertical wall and returns to ground. The total time of flight of the ball is
View SolutionA ball is projected on a very long floor. There may be two conditions (i) floor is smooth &(ii) the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.

Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed u at an angle 30∘ with horizontal and it is known that after collision with the floor its speed becomes u√3 . Then answer the following questions.
If the ball after first collision with the floor has rebounded vertically then the speed of the ball just after the collision with the floor would have been :View SolutionA ball is projected on a very long floor. There may be two conditions (i) floor is smooth &(ii) the collision is elastic
If both the considered then the path of ball is as follows.

Now if collision is inelastic and surface is rough then the path is as follows.

Successive range is decreasing .
Roughness of surface decreases the horizontal component of ball during collision and inelastic nature of collision decreases the vertical component of velocity of ball. In first case both components remain unchanged in magnitude and in second case both the components of the velocity will change.
Let us consider a third case here surface is rough but the collision of ball with floor is elastic. A ball is projected withe speed u at an angle 30∘ with horizontal and it is known that after collision with the floor its speed becomes u√3 . Then answer the following questions.
The angle made by the resultant velocity vector of the ball with horizontal after first collision with floor is :View SolutionA ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.
 View Solution
View Solution

