Two masses m1andm2 are connected by means of a light string, that passes over a light pulley as shown in the figure. If m1=2kgandm2=5kg and a vertical force F is applied on the pulley, then find the acceleration of the masses and that of the pulley when
(a) f = 35N, (b) F = 70N, (c) F = 140N.
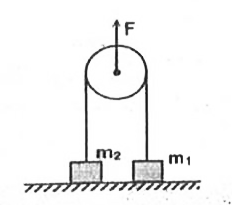
Since string is massless and friction is absent, hence tension in the string is same every where.
(a) Let acceleration of the pulley be ap. For ap to be non-zero, F.B.D. of the pulley
T>m1g ...(1)
⇒T>2g ...(2)
From (1) and (2), we get
F>2×(2g)⇒F>40N
Therefore, when F=35N
ap=0 and hence a1=a2=0
As mass of the pulley is negligible
F−2T=0
⇒T=F/2⇒T=35N
To lift m2,
T≥m2g⇒T≥50N
Therefore, block m2 will not move
⇒T−m1g=m1a1⇒15=2a1
⇒a1=152m/s2
Constraint equation
yp+yp−y1= constant
⇒2yp−y1=c⇒2d2ypdt2−d2y1dt2=0
⇒ap=a12=154m/s2
(c) When F = 140N
T = 70N
⇒T−m1g=m1a1 ...(1)
⇒70N−20N=2×a1⇒a1=25m/s2
T−m2g=m2a2 ...(2)
⇒70N−50N=5a2⇒a2=4m/s2
Constraint equation
yp−y2+yp−y1=c
⇒2yp−y1−y2=c
⇒2d2ypdt2−d2y1dt2−d2y2dt2=0
⇒ap=a1+a22=292m/s2
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - SOLVED PROBLEMS (OBJECTIVE)
17 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION - I
6 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
5 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Numerical Based Type
2 Videos
Similar Questions
Two masses m1 and m2 are connected by means of a light string,that passes over a light pulley as shown in the figure.If m1=2kg and m2=5kg and a vertical force F is applied on the pulley then find the accelerations of the masses and that of the pulley when the force is F=70N
View SolutionTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)

View Solution
Knowledge Check
Two masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
 Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above
Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the aboveTwo masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
 AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)gTwo masses m1 and m2 are attached to a string which passes over a frictionless smooth pulley. When m1=10kg,m2=6kg, the acceleration of masses is
 A20m/s2B5m/s2C2.5m/s2D10m/s2
A20m/s2B5m/s2C2.5m/s2D10m/s2
Two unequal masses of 1kg and 2kg are connected by an inextensible light string passing over a smooth pulley as shown in figure. A force F=20N is applied on 1kg block find the acceleration of either block (g=10m/s2).

View SolutionTwo unequal masses of 1kg and 2kg are connected by an inextensible light string passing over a smooth pulley as shown in figure. A force F=20N is applied on 1kg block find the acceleration of either block (g=10m/s2).

View SolutionTwo masses M and M/ 2 are joint together by means of a light inextensible string passes over a frictionless pulley as shown in figure. When bigger mass is released the small one will ascend with an acceleration of
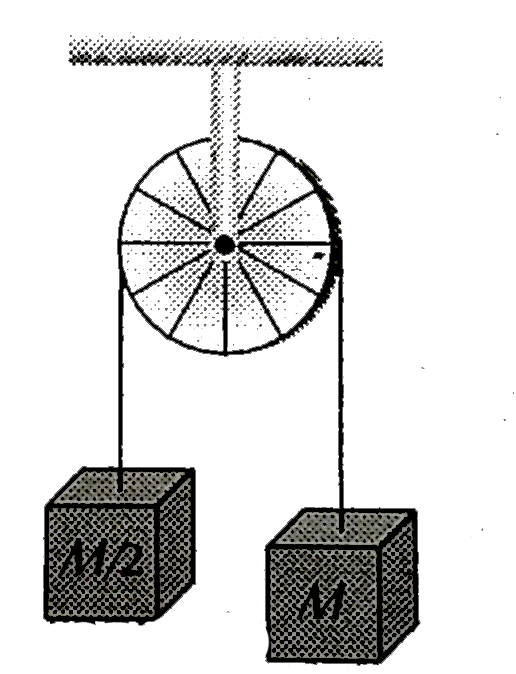
View SolutionTwo masses M and M/ 2 are joint together by means of a light inextensible string passes over a frictionless pulley as shown in figure. When bigger mass is released the small one will ascend with an acceleration of
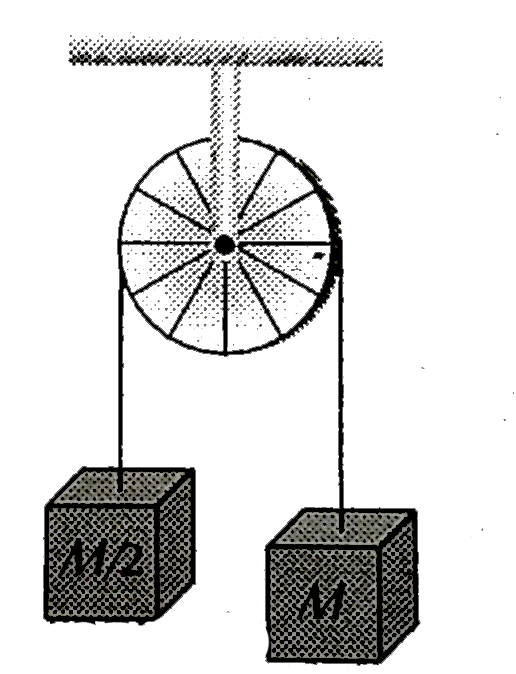
View SolutionTwo masses m1 and m2 are connected by light inextensible string passing over a smooth pulley P. If the pulley moves vertically upwards with an acceleration equal to g then
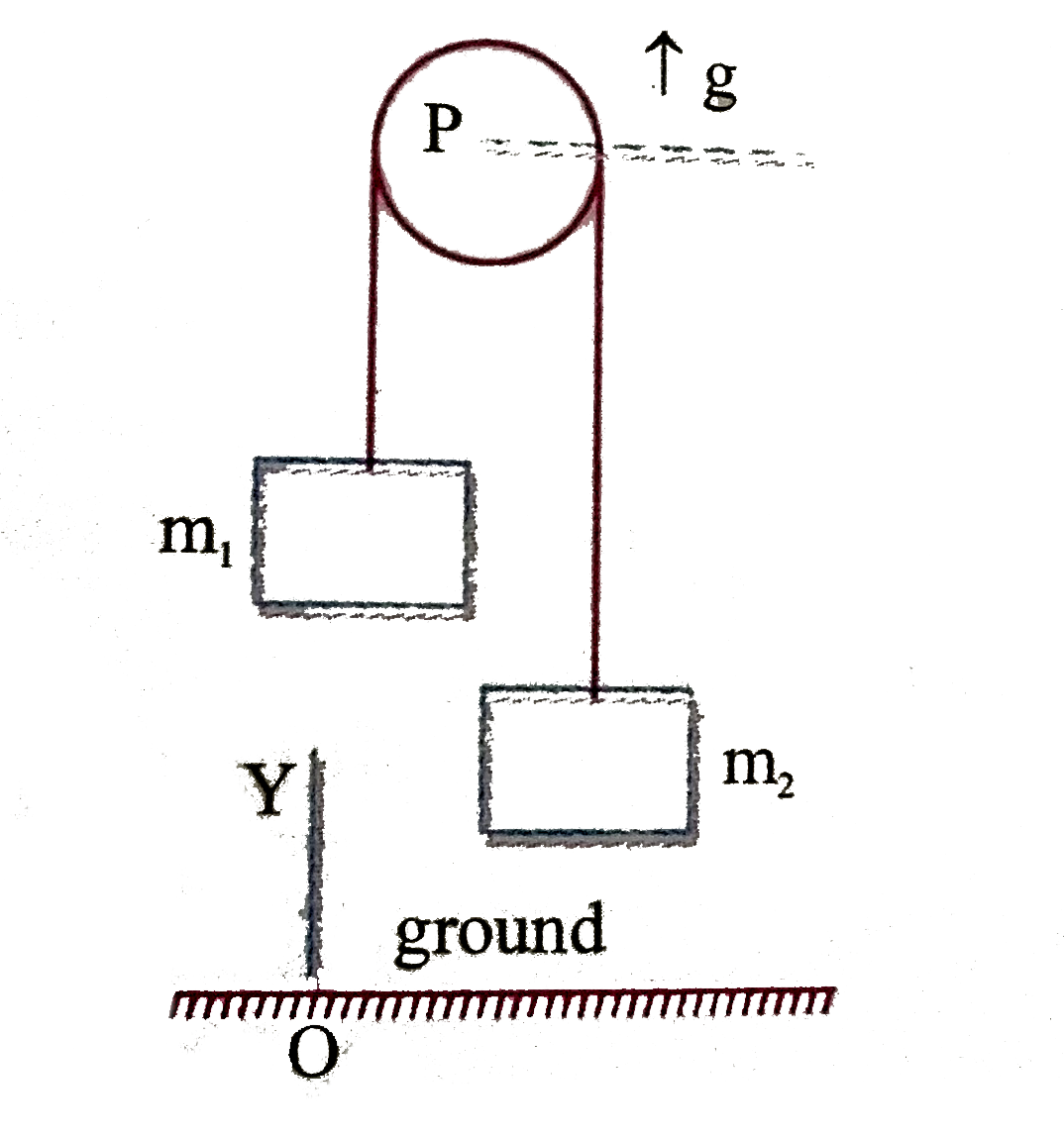 .
.
View Solution
