Two blocks of masses M and m are held on a smooth wedge. The wedge is placed on smooth plane and is free to move on plane. Now both blocks are released, and it is found that block m remains stationary w.r.t. the wedge, the ratio of M/m is 6k. Find the value k.
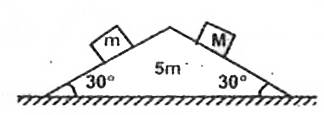
A : acceleration of the wedge w.r.t. the ground. (in leftward direction)
a : acceleration of M w.r.t. the wedge
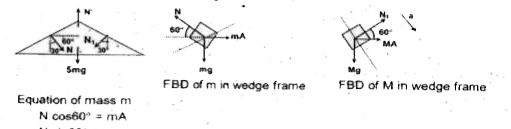
Equation of mass m
Ncos60∘=mA ...(1)
Nsin60∘=mg ...(2)
From equation (2)/(1)
A=gcot60∘=g/√3 ...(3)
Solving (1) and (2)
N=2mg/√3 ...(4)
Equation of the wedge: N1sin30∘−Nsin30∘=5mA (w.r.t. wedge)
N12−mg√3=5mg√3⇒N1=12mg√3
Equation of mass M:N1+MAcos60∘=Mgcos30∘, perpendicular to the wedge.
12mg√3+Mg2√3=√3Mg2⇒M=12m
M:m=12:1
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - MATRIX MATCH TYPE
4 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - Exercise
15 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - ASSERTION REASONING TYPE
1 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
5 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Numerical Based Type
2 Videos
Similar Questions
A block of mass m, is kept on a wedge of mass M, as shown in figure such that mass m remains stationary w.r.t. wedge. The magnitude of force P is

View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View Solution
Knowledge Check
Block of mass m is stationary w.r.t. wedge. Normal force exerted by wedge on the block is
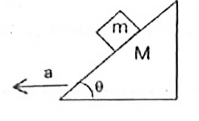 AmgcosθBmgcosθCmgsinθDmgsinθ
AmgcosθBmgcosθCmgsinθDmgsinθA block of mass m is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and theta for the block to remain stationary on the wedge is.
 Aa=gtanθBa=gcosecθCa=cosθDa=gsinθ
Aa=gtanθBa=gcosecθCa=cosθDa=gsinθA block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and for the block to remain stationary on the wedge is:
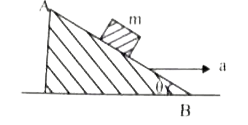 Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθ
Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθ
Two blocks of mass m and 2m are arranged on a wedge that is fixedd on a horizontal surface. Friction coefficient between the block and wedge are shown . Find the magnitude of acceleration of two blocks.

View SolutionA block of mass m is placed at the top of a smooth wedge ABC. The wedge is rotated about an axis passing through C as shown in the figure - 3.81. The minimum value of angular speed ω such that the block does not slip on the wedge is :
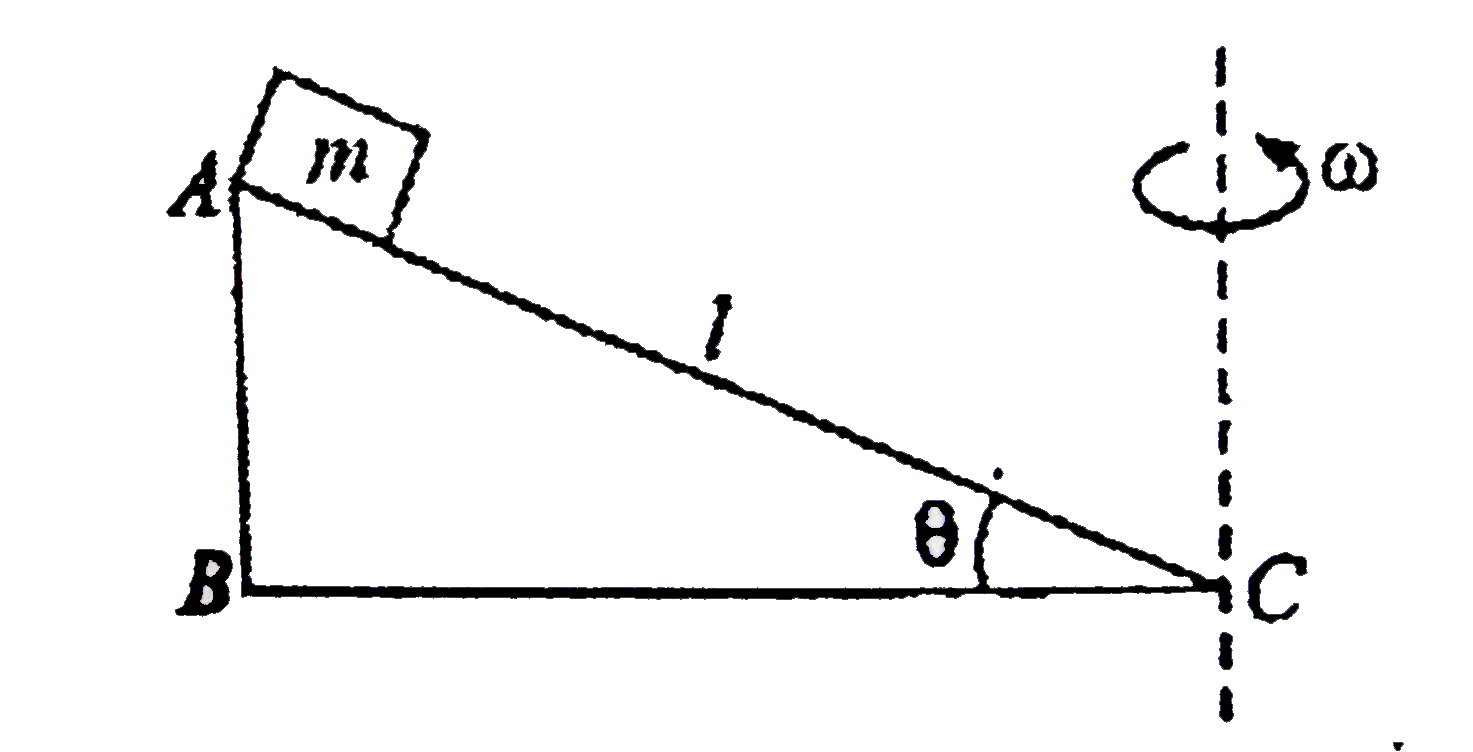
View SolutionA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest

View SolutionA block of mass m is placed on a smooth wedge of wedge angle θ The whole system is accelerated horizontally so that the block does not slip on the wedge. The force (normal reaction) exerted by the wedge on the block has a magnitude:
View SolutionA wooden wedge of mass M and inclination anlgle(α) rest on a smooth floor. A block of mass m is kept on wedge.A force F is applied on the wedge as shown in the figure such that block remains stationary with respect to wedge So, magnitude of froce F is

View Solution
