A pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.
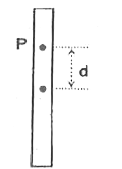
As d changes from L/2 to zero. Time period
increases continuously
decreases continuously
first increases then decrease
first decreases then increase
The correct Answer is:D
Step by step video, text & image solution for A pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown. As d changes from L/2 to zero. Time period by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reason type
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Numerical Based Questions
6 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Solved Problems (Objective)
16 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
A pendulum is formed by pivoting a long thin rod about a point on the rod. In a series of experiments, the period is measured as a function of the distance x between the pivot point and the rod's center. (a) If the rod's length is L= 2.20 m and its mass is m= 22.1g, what is the minimum period? (b) If x is chosen to minimize the period and then L is increased does the period increase, decrease, or remain the same? (c ) If, instead, m is increased without L increasing does the period increase, decrease or remain the same?
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View Solution
Knowledge Check
A pendulum is formed by pivotting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.

As d changes from L/2 to zeroATime period increases continuouslyBTime period decreases continuouslyCTime period first increases then decreaseDTime period first decreases then increaseA pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.
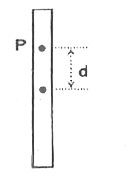
The time period of this pendulum when d = L/2 will beA2π√2l3gB2π√3l2gC4π√l3gD2π3√2lgA pendulum is formed by pivotting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.

The time period of this pendulum when d = L/2 will beA2π√2l3gB2π√3l2gC4π√l3gD2π3√2lg
A pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.
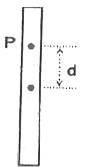
Time period will be minimum when d is equal to
View SolutionA thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is

View SolutionThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L3 from one of its ends and perpendicular to the rod is
View SolutionThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is
View SolutionThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L3 from one of its ends and perpendicular to the rod is
View Solution
