A spring of force constant k = 300 N/m connects two blocks having masses 2 kg and 3kg lying on a smooth horizontal plane. If the spring block system is released from a stretched position find the number of complete oscillations in 1 minute. Take π=√10
The correct Answer is:24
To solve the problem step by step, we will follow these steps:
Step 1: Identify the effective mass of the system
The effective mass μ of two blocks connected by a spring can be calculated using the formula:
μ=m1⋅m2m1+m2
where m1=2kg and m2=3kg.
Step 2: Calculate the effective mass
Substituting the values into the formula:
μ=2⋅32+3=65kg
Step 3: Write the formula for the time period of oscillation
The time period T of the spring-block system is given by:
T=2π√μk
where k=300N/m.
Step 4: Substitute the effective mass and spring constant into the time period formula
Substituting μ and k into the time period formula:
T=2π√65300=2π√61500=2π√1250=2π⋅1√250
Step 5: Simplify the square root
We know that √250=√25⋅10=5√10. Thus:
T=2π⋅15√10=2π5√10
Step 6: Substitute π=√10
Now substituting π=√10:
T=2√105√10=25seconds
Step 7: Calculate the frequency
The frequency f is the reciprocal of the time period:
f=1T=125=52Hz
Step 8: Find the number of complete oscillations in one minute
To find the number of complete oscillations in one minute, we multiply the frequency by 60 seconds:
Number of oscillations in 1 minute=f×60=52×60=150
Final Answer
The number of complete oscillations in one minute is 150.
---
The effective mass μ of two blocks connected by a spring can be calculated using the formula:
μ=m1⋅m2m1+m2
where m1=2kg and m2=3kg.
Substituting the values into the formula:
μ=2⋅32+3=65kg
The time period T of the spring-block system is given by:
T=2π√μk
where k=300N/m.
Substituting μ and k into the time period formula:
T=2π√65300=2π√61500=2π√1250=2π⋅1√250
We know that √250=√25⋅10=5√10. Thus:
T=2π⋅15√10=2π5√10
Now substituting π=√10:
T=2√105√10=25seconds
The frequency f is the reciprocal of the time period:
f=1T=125=52Hz
To find the number of complete oscillations in one minute, we multiply the frequency by 60 seconds:
Number of oscillations in 1 minute=f×60=52×60=150
The number of complete oscillations in one minute is 150.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Subjective) (Level-II & III)13videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-I)39videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise28videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I20videos
SEMICONDUCTOR AND DEVICE
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
Similar Questions
A spring of force constant k = 300 N/m connects two blocks having masses 2 kg and 3kg lying on a smooth horizontal plane. If the spring block system is released from a stretched position find the number of complete oscillations in 1 minute. Take π=√10
View SolutionTwo blocks rest on a smooth horizontal surface. They are connected by a spring of force constant k. If the system is set into oscillation find its time period.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied on a 1-kg block. Find the force of interaction of the blocks.

A4NB5NC10NDnone - Question 2 - Select One or More
Two blocks of mass m1 and m2, resting on a frictionless table, are connected by a stretched spring and then released -
Aratio of speed of blocks is m2/m1Bratio of kinetic energy of blocks is m2/m1Ccentre of mass will move towards heavier blockDmechanical energy will remain conserve in this process - Question 3 - Select One
A spring of force constant k is cut into two parts whose lengths are in the ratio 1:2. The two parts are now connected in parallel and a block of mass m is suspended at the end of the combined spring. The period of oscillation of block is
A2π√2m9KB2π√m9KC2π√2m5KD2π√m5K
Figure shows two block A and B, each having a mass of 320 g connected by a light string passing over a smooth light pulley. The horizontal surface on which the block A can slide is smooth. The block A is attached to spring constant 40N/m whose other end is fixed to a support 40 cm above the horizontal surface. Initially, the spring is vertical and unstretched when the system is released to move. Find the velocity of the block A at the instant it breaks off the surface below it. Take g=10m/s2 .
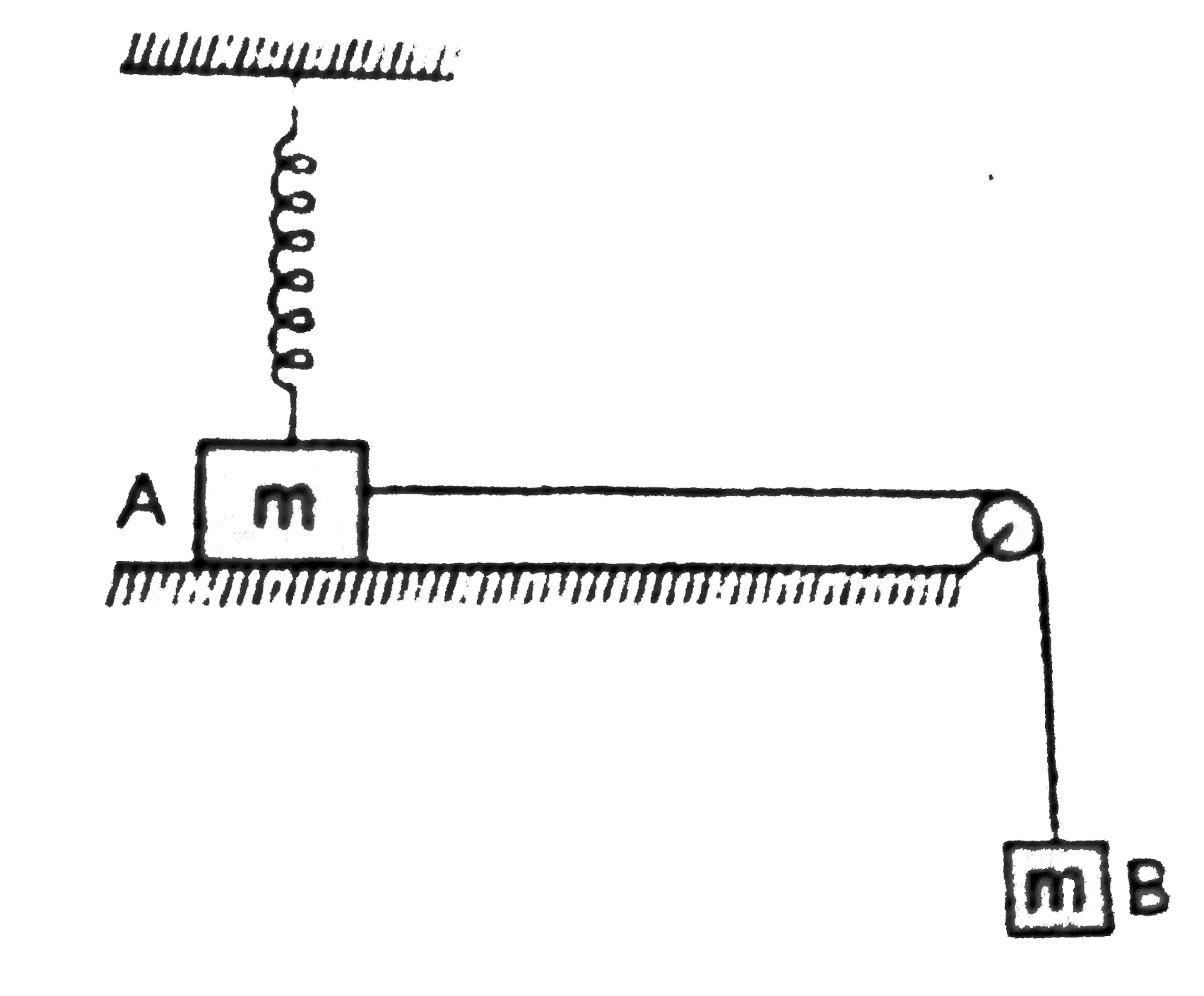 View Solution
View SolutionA block of mass m connected with a smooth prismatic wedge of mass m is released from rest when the spring is relaxed. Find the angular frequency of oscillation.
 View Solution
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.
 View Solution
View SolutionThree blocks of masses m1=10kg,m2=20kg,m3=30kg are connected by strings on smooth horizontal surface and pulled by a force of 60 N. Find the acceleration of the system and tensions in the string.
 View Solution
View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
View Solution

