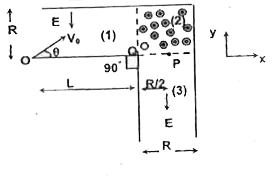
The diagram shows combination of three cuboidal spaces (1),(2) and (3). Space 1 and 3 contain electric field E as shown while space 2 has magnetic field B. A particle of charge q and mass m is projected as shown with velocity V0cosθ(i)+V0sinθˆj. Find the value of E, so that his particle enters the magnetic field parallel to the x-axis and just passes through point P along the electric field at that point. Find its speed at P and also the ratio L/R (Neglect the effect of gravity)
The correct Answer is:mV20sin2θ2qL,V0cosθ,cotθ
Topper's Solved these Questions
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Assignment Problems (Objective) (LEVEL-I)
50 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Assignment Problems (Assertion Reasoning Type)
2 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Assignment Problems (Subjective) (Level-I)
15 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
- MAGNETISMBOOK - FIITJEECHAPTER - MAGNETISMEXERCISE - Example
12 Videos
Similar Questions
A positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find

distance travelled in the magnetic field
View SolutionThere exist uniform magnetic field →B=−B0ˆk in region of space with 0<x<d and 2d<x<3d as shown in the figure. A positive charged particle of mass m and charge q is projected with velocity →v=vˆi as shown in the figure. If radius of curvature of path of the charged particle in magnetic field isR(2d<R<3d) then time elapse by charged particle in magnetic field regions is

View Solution
Knowledge Check
A uniform magnetic field B=B0ˆj exists in space. A particle of mass m and charge q is projected towards X-axis with speed v from a point (a,0, 0). The maximum value of v for which the particle does not hit the Y-Z plane is
ABqamBBqa2mCBqamDBq2amThe electric field acts positive x-axis. A charged particle of charge q and mass m is released from origin and moves with velocity →v=v0ˆj under the action of electric field and magnetic field, →B=B0ˆi. The velocity of particle becomes 2v0 after time √3mv0√2qE0. find the electric field:
A√2√3E0ˆiB√3√2E0ˆiC(√3)E0ˆiD(√2)E0ˆiThere exist uniform magnetic field →B=−B0ˆk in region of space with 0<x<d and 2d<x<3d as shown in the figure. A positive charged particle of mass m and charge q is projected with velocity →v=vˆi as shown in the figure. If radius of curvature of path of the charged particle in magnetic field isR(2d<R<3d) then time elapse by charged particle in magnetic field regions is
 Am2qBB2mqBsin−1(dR)CmqBDmqBsin−1(dR)
Am2qBB2mqBsin−1(dR)CmqBDmqBsin−1(dR)
In a certain region, uniform electric field E=−E0ˆk and magnetic field B=B0ˆk are present. At time t=0, a particle of mass m and charge q is given a velocity v=vj+vk. Find the minimum speed of the particle and the time when it happens so.

View SolutionIn a certain region, uniform electric field E=−E0ˆk and magnetic field B=B0ˆk are present. At time t=0, a particle of mass in and charge q is given a velocity v=v−0ˆj+v−0ˆk. Find the minimum speed of the particle and the time when it happens so.

View SolutionElectric field and magnetic field n a region of space is given by E=E0ˆj and B=B0ˆj. A particle of specific charge alpha is released from origin with velocity v=v0ˆi. Then path of particle
View SolutionA uniform magnetic field ¯¯¯B=B0ˆj exists in a space. A particle of mass m and charge q is projected towards negative x-axis with speed v from the a point (d,0,0) The maximum value v for which the particle does not hit y−z plane is .
View SolutionThere exist uniform magnetic field →B=−B0ˆk in region of space with 0<x<d and 2d<x<3d as shown in the figure. A positive charged particle of mass m and charge q is projected with velocity →v=vˆi as shown in the figure. If radius of curvature of path of the charged particle in magnetic field isR(2d<R<3d) then time elapse by charged particle in magnetic field regions is

View Solution
