A point source of light B is placed at a distance L in front of the centre of a mirror of width d hung vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance 2L from it as shown. The greatest distance over which he can see the image of the light source in the mirror is
d2
d
2d
3d
The correct Answer is:D
To solve the problem, we need to analyze the situation involving the point source of light, the mirror, and the position of the man walking in front of the mirror.
1. Understanding the Setup:
- We have a point source of light B located at a distance L in front of the center of a vertical mirror.
- The mirror has a width d.
- The man is walking parallel to the mirror at a distance of 2L from it.
2. Finding the Image of the Light Source:
- The image of the point source B will be formed behind the mirror at a distance L (the same distance as the object) from the mirror.
- Thus, the image B' is located at a distance L behind the mirror.
3. Determining the Viewing Angles:
- To determine the greatest distance over which the man can see the image of the light source, we need to consider the angles formed by the lines of sight from the man to the edges of the mirror.
- The man can see the image of the light source as long as his line of sight to the edges of the mirror is unobstructed.
4. Using Similar Triangles:
- Let’s denote the position of the man as point M, which is at a distance of 2L from the mirror.
- The line of sight from the man to the top and bottom edges of the mirror will form two triangles with the mirror.
- These triangles are similar to the triangle formed by the image and the edges of the mirror.
5. Calculating the Total Viewing Distance:
- The width of the mirror is d.
- Since the triangles are similar, the ratio of the height to the base will be the same.
- The distance from the man to the point where he can just see the edges of the mirror can be calculated using the width of the mirror and the distance from the man to the mirror.
- The total distance over which he can see the image of the light source is given by the formula:
Total Viewing Distance=2×(d2L×2L)=d
6. Final Result:
- Therefore, the greatest distance over which the man can see the image of the light source in the mirror is 3d.
Conclusion:
The answer to the question is 3d.
- We have a point source of light B located at a distance L in front of the center of a vertical mirror.
- The mirror has a width d.
- The man is walking parallel to the mirror at a distance of 2L from it.
- The image of the point source B will be formed behind the mirror at a distance L (the same distance as the object) from the mirror.
- Thus, the image B' is located at a distance L behind the mirror.
- To determine the greatest distance over which the man can see the image of the light source, we need to consider the angles formed by the lines of sight from the man to the edges of the mirror.
- The man can see the image of the light source as long as his line of sight to the edges of the mirror is unobstructed.
- Let’s denote the position of the man as point M, which is at a distance of 2L from the mirror.
- The line of sight from the man to the top and bottom edges of the mirror will form two triangles with the mirror.
- These triangles are similar to the triangle formed by the image and the edges of the mirror.
- The width of the mirror is d.
- Since the triangles are similar, the ratio of the height to the base will be the same.
- The distance from the man to the point where he can just see the edges of the mirror can be calculated using the width of the mirror and the distance from the man to the mirror.
- The total distance over which he can see the image of the light source is given by the formula:
Total Viewing Distance=2×(d2L×2L)=d
- Therefore, the greatest distance over which the man can see the image of the light source in the mirror is 3d.
The answer to the question is 3d.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - OPTICSEXERCISE - ASSERTION REASONING TYPE3videos
OPTICS
- BOOK - FIITJEECHAPTER - OPTICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE)(level 2)20videos
OPTICS
- BOOK - FIITJEECHAPTER - OPTICSEXERCISE - assignment problem(subjective)(Level - II & III)15videos
OPTICS
- BOOK - FIITJEECHAPTER - MODERN PHYSICSEXERCISE - Numerical based questions5videos
MODERN PHYSICS
- BOOK - FIITJEECHAPTER - PHYSICS PART-IIIEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE11videos
PHYSICS PART-III
Similar Questions
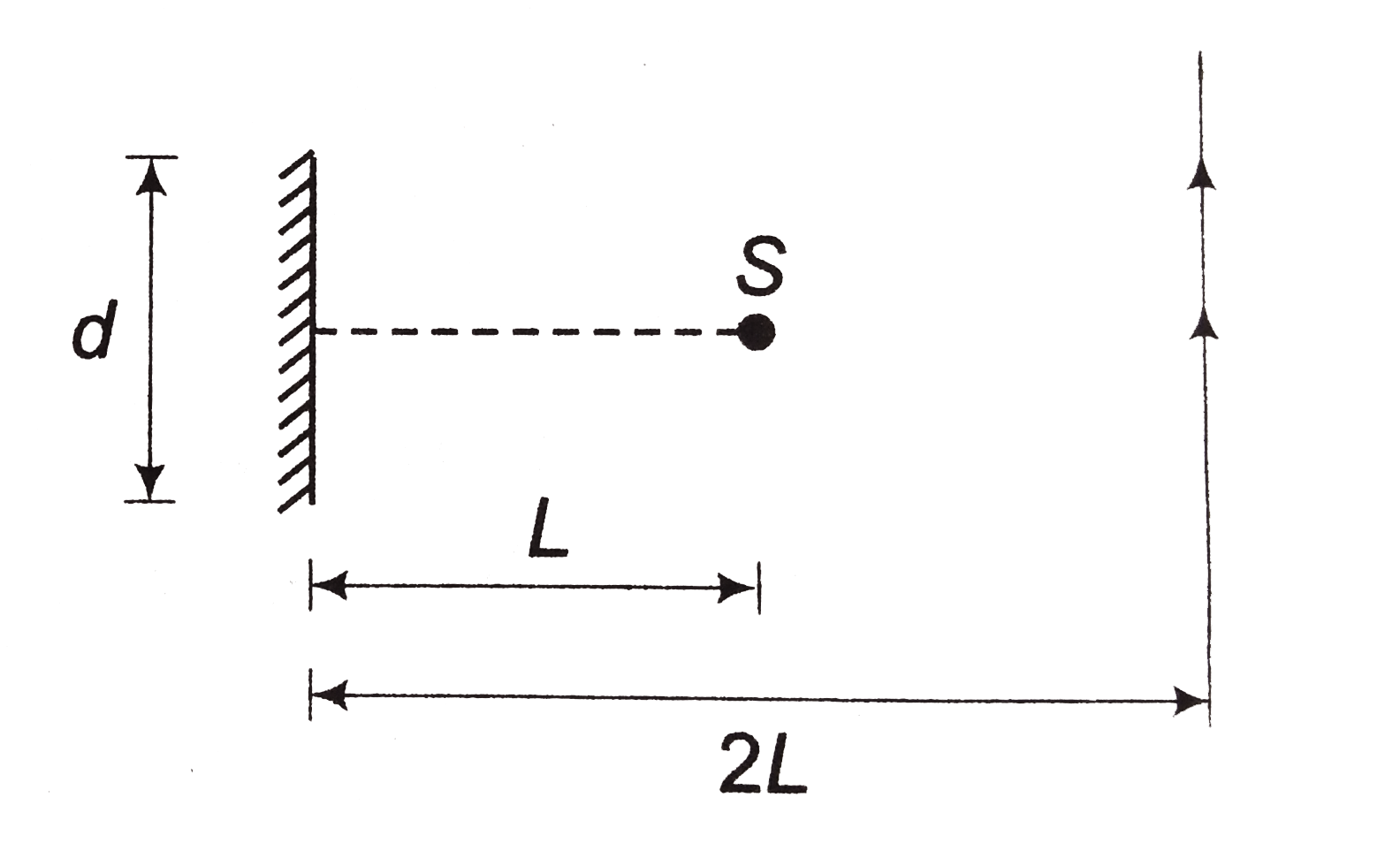
A point source of light S, placed at a
distance L in front of the centre of a mirror of width d,
hangs vertically on a wall. A man walks in front of the
mirror along a line parallel to th mirror at a distance
2L form it as shown. The greatest distance over which
he can see the image of the light source in the mirror is
(a) d/2 (b) d (c) 2d (d) 3 d.
 View Solution
View SolutionA point source of light B is placed at a distance L in front of the centre of a mirror of which d hung vertically on a wall.A man walks in front of the mirror along a line parallel to the mirror at a distance 2L from it as shown in figure . The greatest distance over which he can see the image of the light source in mirror is :

[3d]View Solution
Knowledge Check
- Question 1 - Select One
A point source of light B is placed at a distance L in front of the centre of a mirror of width d hung vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance 2L from it as shown in fig. The greatest distance over which he can see the image of the light source in the mirror is
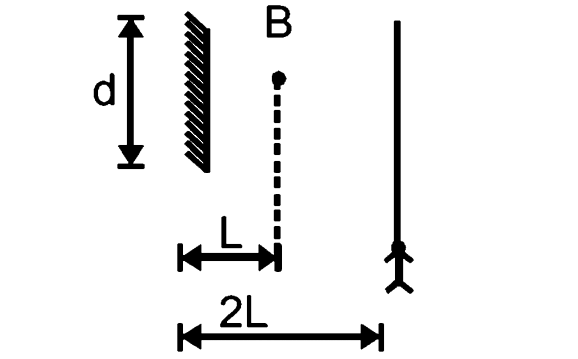 Ad2BdC2dD3d
Ad2BdC2dD3d - Question 2 - Select One
A point source of light B is placed at a distance L in front of the center of a mirror of width d hung vertically on a wall. A man walks in front of mirror along a line parallel to the mirror at a distance 2L from it as shown in Figure. The greatest distance over which he can see the image of the light source in the mirror is
 Ad/2BdC2dD3d
Ad/2BdC2dD3d - Question 3 - Select One
A point source of light B is placed at a distance L in front of the center of a mirror of width 'd' hung vertically on a wall. A man walks in front of the mirror along a line parallel to the mirro at a distance 2L from it as shown in figure. The greatest distance over which he can see the image of the light source in the mirror is
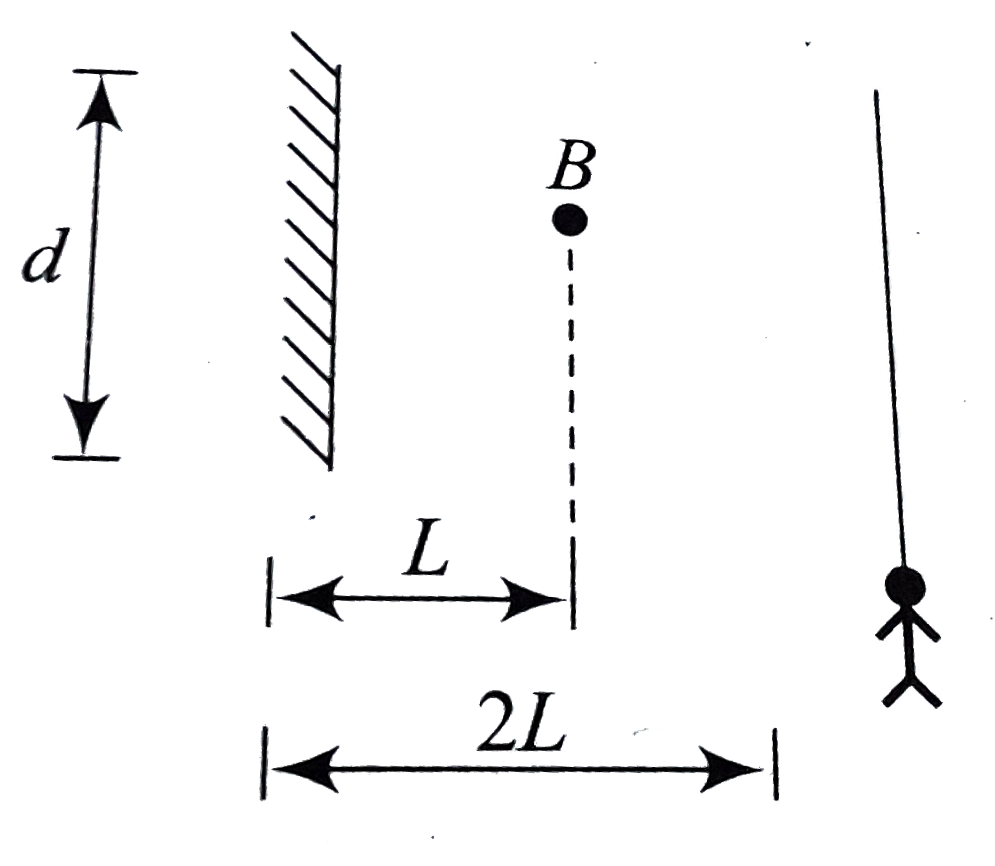 Ad/2BdC2dD3d
Ad/2BdC2dD3d
A point source of light B is placed at a distance L in front of the center of a mirror of width d hung vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance 2L from it, as shown in Fig . Find the greated distance over which he can see the image of the light source form the mirror.
 View Solution
View SolutionA point source of light, S is placed at a distance L in front of the centre of plane mirror of width d which is hanging vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror, at a distance 2L as shown below. The distance over which the man can see the image of the light source in the mirror is nd then value of n is :
 View Solution
View SolutionA point source of light ,S is placed at a distance L in front of the centre of plane mirror of width d which is a hanging vertically on wall ,A man walks in front of the mirror , at a distance 2L as shown below . The distance over which the man can see the image of the light source in the mirror is :
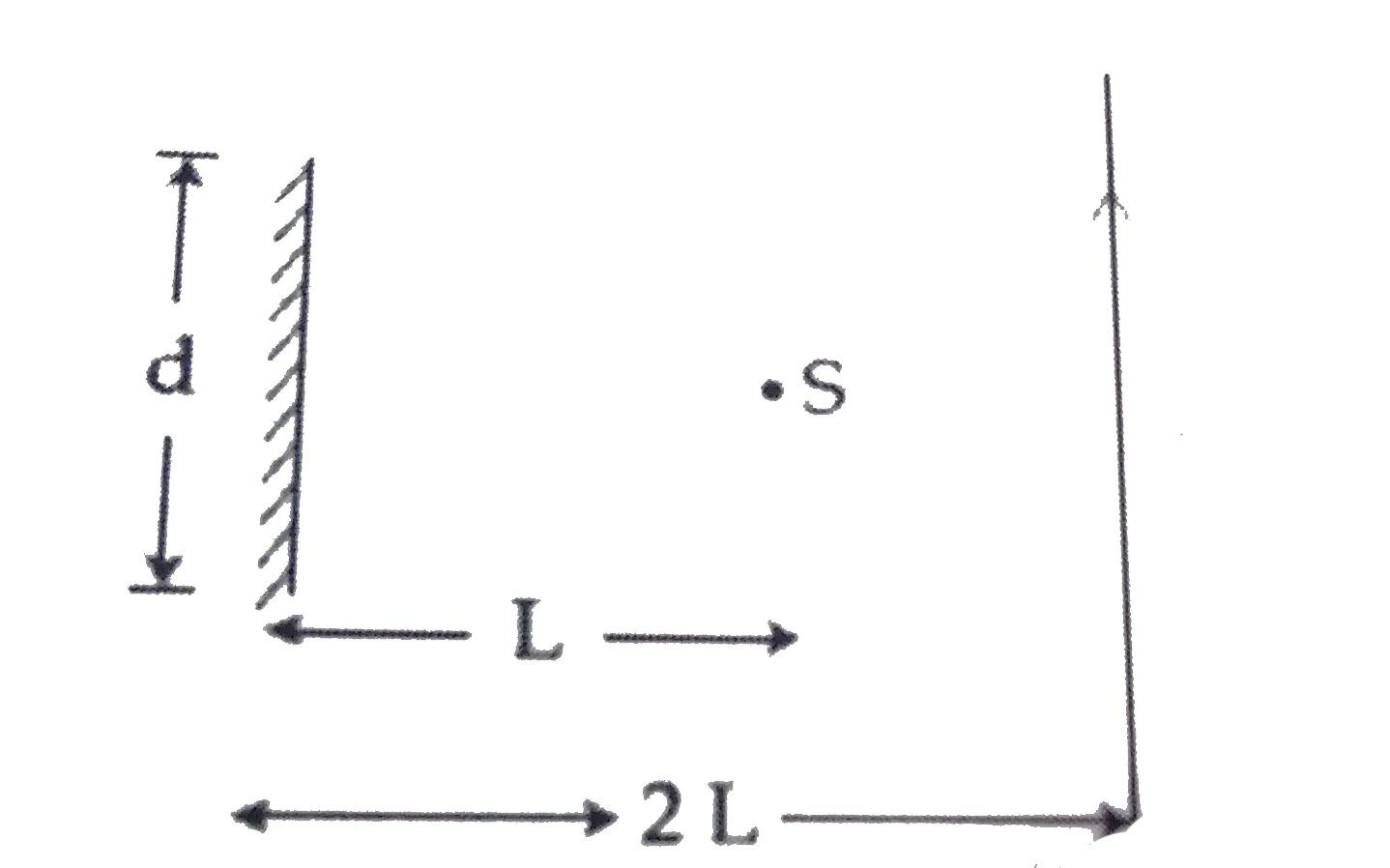 View Solution
View SolutionA point source of light S, placed at a distance 60 cm infront of the centre of a plane mirror of width 50 cm, hangs vertically on a wall. A man walks infront of the mirror along a line parallel to the mirror at a distance 1.2 m from it (see in the figure). The distance between the extreme points where he can see the image of the light source in the mirror is .......... cm.
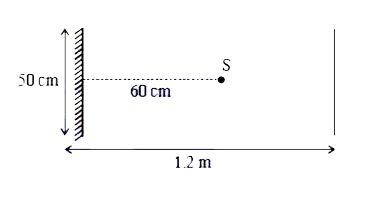 View Solution
View SolutionA point source of light S is placed at a distance 10 cm in front of the centre of a mirror of width 20 cm suspended vertically on a wall. An insect walks with a speed 10cm/s in front of the mirror along a line parallel to the mirror at a distance 20 cm from it as shown in figure. find the maximum time during which the insect can see the image of the source S in the mirror.
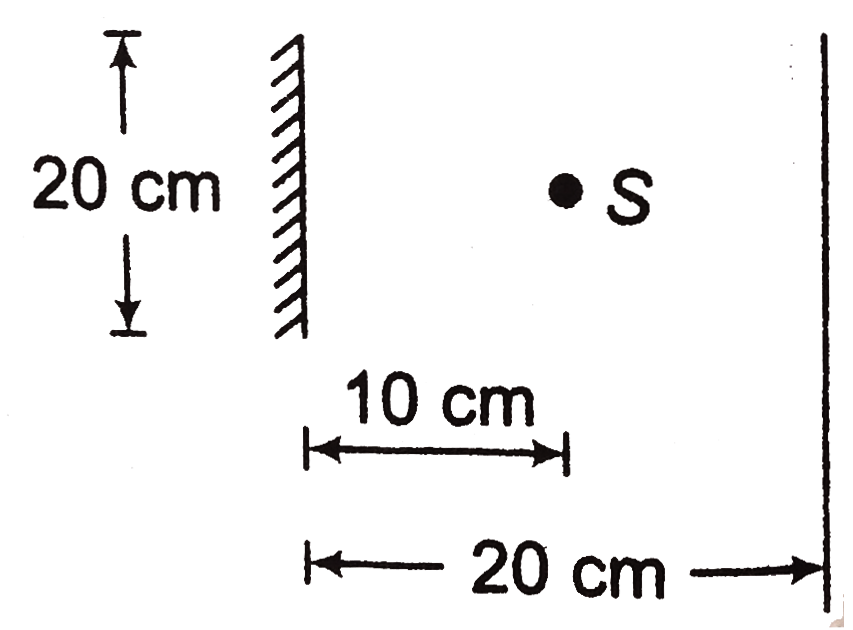 View Solution
View Solution

