Read the paragraph carefully and answer the following questions:
Real gases deviate from ideal behaviour because of the following two faulty assumptions of kinetic theory.
(I) The actual volume occupied by molecules is negligible as compared to the total volume of the gas.
(II) The forces of attraction and repulsion between molecules of the gas are negligible. The extent of deviation of a real gas from ideal behaviour is expressed in terms of compressibility factor (z).
Hence, suitable corrections were applied to the ideal gas equation so that it can also explain the behaviour of real gases. The equation obtained by applying the two corrections to the usual gas equation is known as van der Waal equation.
A Volume correction Corrected (ideal) volume = (V - b) Where b is the effective volume of the molecules.
B. Pressure correction (intermolecular attraction corection). Corrected (ideal) pressure = P + P
However, P=aV2
∴ The van der Waal's equation becomes (P+an2V2)(V−nb)=nRT
van der Waal equation is obeyed by the real gases
The correct Answer is:A
Topper's Solved these Questions
- GASEOUS STATEBOOK - FIITJEECHAPTER - GASEOUS STATEEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II COMPREHENSION-II
4 Videos
- GASEOUS STATEBOOK - FIITJEECHAPTER - GASEOUS STATEEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II COMPREHENSION-III
5 Videos
- GASEOUS STATEBOOK - FIITJEECHAPTER - GASEOUS STATEEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II
20 Videos
- ENVIRONMENTAL CHEMISTRYBOOK - FIITJEECHAPTER - ENVIRONMENTAL CHEMISTRYEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL -II (MULTIPLE CORRECT QUESTIONS)
20 Videos
- GENERAL ORGANIC CHEMISTRYBOOK - FIITJEECHAPTER - GENERAL ORGANIC CHEMISTRYEXERCISE - SINGLE INTEGER ANSWER TYPE QUESTIONS
14 Videos
Similar Questions
Read the following paragraph and answer the questions given below:
According to Maxwell distribution, the area under the curve is equal to the total number of molecules in collision. On increasing temperature, fraction of molecules having speed equal to ump (most probable speed) decreases. The speed distribution also depends on the mass of the molecules along with the temperature.
In general, the distribution depends upon the value of MT (where M is molar mass and T is temperature in kelvin).
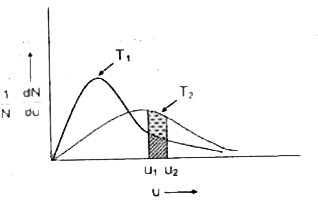
Choose the correct option:
Relationship between T1andT2 a is given as
View SolutionRead the paragraph carefully and answer the following questions:
During gas analysis, the eudiometer tube filled with mercury is inverted over a trough containing. mercury. A known volume of the gas. or gaseous mixture to be studied is next introduced, which displaces an equivalent amount of mercury. Next a known amount, of oxygen in excess is introduced and the electric spark is passed, whereby the combustible material gets oxidized. The volume of carbon dioxide, water vapour or other gaseous products of combustíon are next determined by absorbing them in suitable reagents. The various reagents used for absorbing different gases areO3→ turpentine oil
O2→ alkalino pyragallol
CO2,SO2→ alkali solution [NaOH,KOH,Ca(OH)2]
0.2 mole sample of hydrocarbon CxHy yields after complete combustion with excess O2 gas, 0.8 mole of CO2, 1.1 mole of H2O. Hence,, hydrocarbon is
View SolutionVav,VrmsandVmp are average speed, root mean square speed and most probable speed of the gas respectively at constant temp. T. Molar mass of gas is 'm'. Then
View SolutionWhich of the following act as secondary pollutants ?
View SolutionHow many electrons occupy the bonding molecular orbitals of a C:N triple bond?
View SolutionReal gases deviated from ideal behaviour due to the following two faulty assumptions of kinetic theory of gases : (i) Actual volume occupied by the gas molecule is negligible as compared to the total volume of the gases (ii) Forces of attraction and repulsion among gas molecules are negligible To explain the extent of deviation of the real gas from ideal behaviour in terms of compressibility or compression factor (z) , which is the function of pressure and temperature for real gases z = (P_(0)V_(0))/(nRT) For ideal gases z = 1 . for real gases either z gt 1 " or " z gt 1 . When z gt 1 , then it is less compressible because force of repulsion dominates over force of attraction. When z lt 1 , force of attraction dominates over the repulsion and it is more compressible. Graph in between z and P is shown below on increasing the temperature, z increases and approaches to unity. Graph between z and p at different temperature are as under Answer the following questions on the basis of above write up : Which of the following is the correct order of temperature shown in the above graph z vs P for the same gas
View SolutionReal gases deviated from ideal behaviour due to the following two faulty assumptions of kinetic theory of gases :
(i) Actual volume occupied by the gas molecule is negligible as compared to the total volume of the gases
(ii) Forces of attraction and repulsion among gas molecules are negligible
To explain the extent of deviation of the real gas from ideal behaviour in terms of compressibility or compression factor (z), which is the function of pressure and temperature for real gases z=P0V0nRT For ideal gases z=1. for real gases either z>1 or z>1.
When z>1, then it is less compressible because force of repulsion dominates over force of attraction. When z<1, force of attraction dominates over the repulsion and it is more compressible.
Graph in between z and P is shown below on increasing the temperature, z increases and approaches to unity. Graph between z and p at different temperature are as under

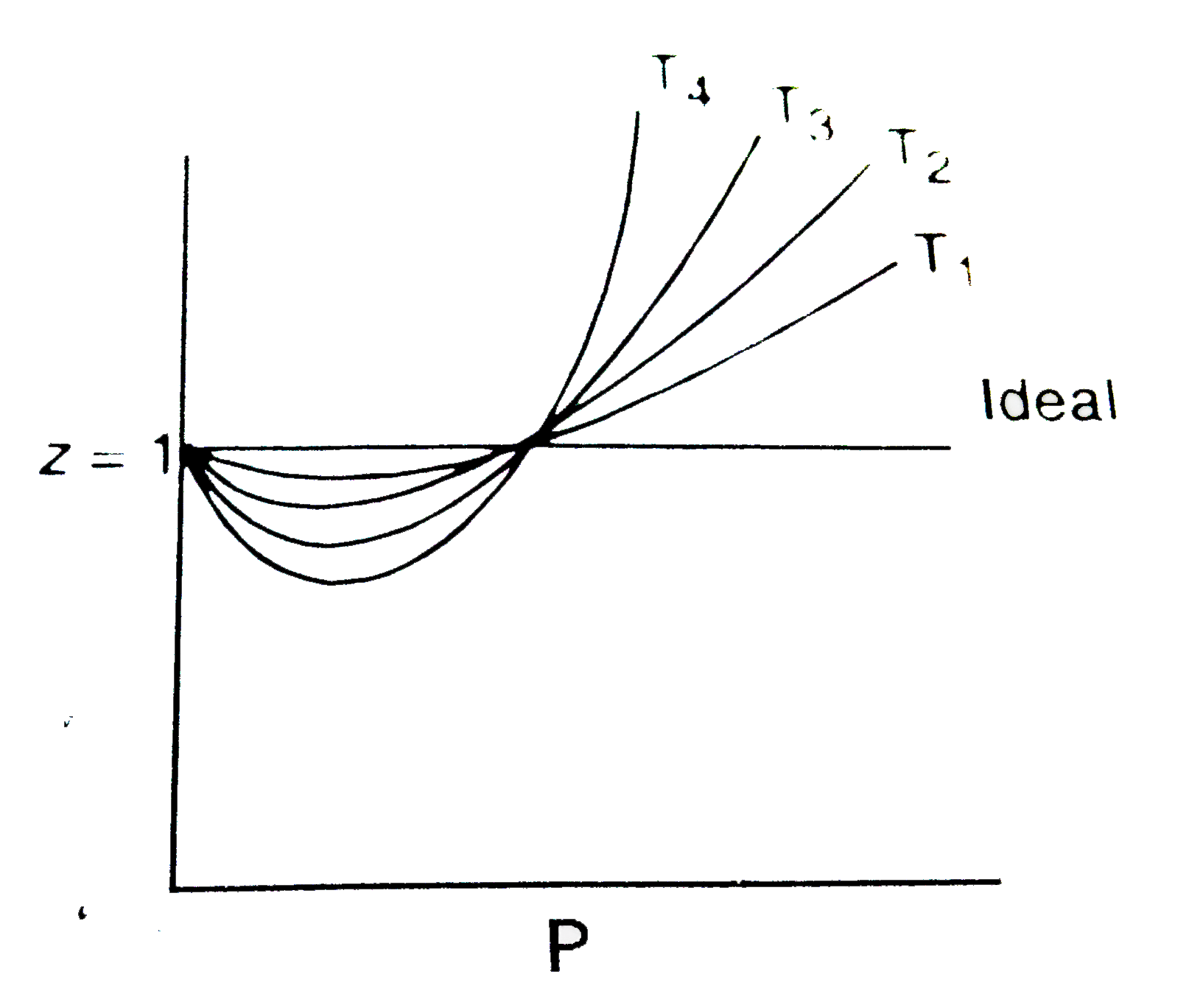
Answer the following questions on the basis of above write up :
Which of the following statements is correct gas A having molar mass 16 g and density 0.75 g/litre at 2 atmospheric pressure and 27∘C temperature
View SolutionThe main reason for deviation of gases from ideal behaviour is few assumptions of kinetic theory . These are
(i) there is no force of attraction between the molecules of a gas
(ii) volume of the molecules of a gas is negligibly small in comparison to the volume of the gas
(iii) particles of a gas are always in constant random motion .
View SolutionGases deviate from the ideal gas behaviour because their molecules
View SolutionBehaviour Of Real Gases | Deviation From Ideal Gas Behaviour | Part 1
View SolutionBehaviour Of Real Gases | Deviation From Ideal Gas Behaviour | Part 2
View SolutionRead the paragraph carefully and answer the following questions: Real gases deviate from ideal behaviour because of the following two faulty assumptions of kinetic theory. (I) The actual volume occupied by molecules is negligible as compared to the total volume of the gas. (II) The forces of attraction and repulsion between molecules of the gas are negligible. The extent of deviation of a real gas from ideal behaviour is expressed in terms of compressibility factor (z). Hence, suitable corrections were applied to the ideal gas equation so that it can also explain the behaviour of real gases. The equation obtained by applying the two corrections to the usual gas equation is known as van der Waal equation. A Volume correction Corrected (ideal) volume = (V - b) Where b is the effective volume of the molecules. B. Pressure correction (intermolecular attraction corection). Corrected (ideal) pressure = P + P However, P=(a)/(V^(2)) therefore The van der Waal's equation becomes (P+(an^(2))/(V^(2)))(V-nb)=nRT 0.5 value of compressibility factor (z) indicates that the gas
View SolutionRead the paragraph carefully and answer the following questions: Real gases deviate from ideal behaviour because of the following two faulty assumptions of kinetic theory. (I) The actual volume occupied by molecules is negligible as compared to the total volume of the gas. (II) The forces of attraction and repulsion between molecules of the gas are negligible. The extent of deviation of a real gas from ideal behaviour is expressed in terms of compressibility factor (z). Hence, suitable corrections were applied to the ideal gas equation so that it can also explain the behaviour of real gases. The equation obtained by applying the two corrections to the usual gas equation is known as van der Waal equation. A Volume correction Corrected (ideal) volume = (V - b) Where b is the effective volume of the molecules. B. Pressure correction (intermolecular attraction corection). Corrected (ideal) pressure = P + P However, P=(a)/(V^(2)) therefore The van der Waal's equation becomes (P+(an^(2))/(V^(2)))(V-nb)=nRT The pressure correction used on the ideal gas behaviour is generally indicated by P +P what does this P' stand for
View SolutionRead the paragraph carefully and answer the following questions: Real gases deviate from ideal behaviour because of the following two faulty assumptions of kinetic theory. (I) The actual volume occupied by molecules is negligible as compared to the total volume of the gas. (II) The forces of attraction and repulsion between molecules of the gas are negligible. The extent of deviation of a real gas from ideal behaviour is expressed in terms of compressibility factor (z). Hence, suitable corrections were applied to the ideal gas equation so that it can also explain the behaviour of real gases. The equation obtained by applying the two corrections to the usual gas equation is known as van der Waal equation. A Volume correction Corrected (ideal) volume = (V - b) Where b is the effective volume of the molecules. B. Pressure correction (intermolecular attraction corection). Corrected (ideal) pressure = P + P However, P=(a)/(V^(2)) therefore The van der Waal's equation becomes (P+(an^(2))/(V^(2)))(V-nb)=nRT At low pressure, the van der waal equation is
View SolutionRead the paragraph carefully and answer the following questions: Real gases deviate from ideal behaviour because of the following two faulty assumptions of kinetic theory. (I) The actual volume occupied by molecules is negligible as compared to the total volume of the gas. (II) The forces of attraction and repulsion between molecules of the gas are negligible. The extent of deviation of a real gas from ideal behaviour is expressed in terms of compressibility factor (z). Hence, suitable corrections were applied to the ideal gas equation so that it can also explain the behaviour of real gases. The equation obtained by applying the two corrections to the usual gas equation is known as van der Waal equation. A Volume correction Corrected (ideal) volume = (V - b) Where b is the effective volume of the molecules. B. Pressure correction (intermolecular attraction corection). Corrected (ideal) pressure = P + P However, P=(a)/(V^(2)) therefore The van der Waal's equation becomes (P+(an^(2))/(V^(2)))(V-nb)=nRT The values of van der Waal's constant 'a' ("atm"^(2) L^(2)" mol"^(2)) for the gases N_(2), H_(2) NH_(3) and SO_(2) are given 0.25, 3.5, 4,9 and 6.9 respectively. Which will have the highest ease of liquefaction?
View Solution
