For the reaction AK1⇐===⇒K2B, if 'a' is the initial concentration of A and n is the number of moles of A reacting if initially no B was present then :
dxdt=[K1(a−x)−K2x] initially
K1(a−xe)−K2xe=0 at equilibrium
K1+K2=K1.axe
(K1+K2)=1tln.xexe−x
The correct Answer is:A, B, C, D
Initially, dxdt=K1(a−x)−K2x………(1)
Hence choice (A) is correct.
If xe= equilibrium concentration of B, where net rate =0
K1(a−xe)−K2xe=0………..(2)
Hence choice (B) is correct.
From equation (2) , K2=K1(a−xe)xe
Substituting the value of K2 in equation (1), we get
dxdt=K1(a−x)−K1(a−xe)xxe
=K1(xe−x)axe
⇒dx(xe−x)=axeK1dt
Hence by integrating and further calculation, we get
(K1+K2)=K1axe=1tln.xe(xe−x)
Topper's Solved these Questions
- CHEMICAL KINETICS AND RADIOACTIVITYBOOK - FIITJEECHAPTER - CHEMICAL KINETICS AND RADIOACTIVITYEXERCISE - Comprehension I
3 Videos
- CHEMICAL KINETICS AND RADIOACTIVITYBOOK - FIITJEECHAPTER - CHEMICAL KINETICS AND RADIOACTIVITYEXERCISE - Comprehension II
2 Videos
- CHEMICAL KINETICS AND RADIOACTIVITYBOOK - FIITJEECHAPTER - CHEMICAL KINETICS AND RADIOACTIVITYEXERCISE - Solved problem (subjective)
15 Videos
- CHEMICAL EQUILIBRIUMBOOK - FIITJEECHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - MATCHING TYPE QUESTIONS
3 Videos
- CHEMISTRY IN EVERY DAY LIFE BOOK - FIITJEECHAPTER - CHEMISTRY IN EVERY DAY LIFE EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - II (Numerical Based Questions)
5 Videos
Similar Questions
In a reversible reaction AK1⇐⇒K2B the initial concentration of A and B are a and b in moles per litre and the equilibrium concentrations are (a-x) and (b+x) respectively, Express x in terms of K1,K2,aandb.
View SolutionIn a chemical reaction , A+2BK⇐⇒2c+D, the initial concentration of B was 1.5 times of the concentrations of A , but the equilibrium concentrations of A and B were found to be equal . The equilibrium constant (K) for the aforesaid chemical reaction is :
View Solution
Knowledge Check
For the reaction, H2+I2k1⇐⇒k22HI. The rate law expression is :
A[−12d[HI]dt]=k1[H2][I2]B[−12d[HI]dt]=k1[HI]2k2[H2][I2]C[−12d[HI]dt]=k1[H2][I2]−k2[HI]2D[−12d[HI]dt]=k1k2[H2][I2]In a reversible reaction AK1⇐⇒K2B the initial concentration of A and B are a and b in moles per litre and the equilibrium concentrations are (a-x) and (b+x) respectively, Express x in terms of K1,K2,aandb.
AK1a−K2bK1+K2BK1a−K2bK1−K2CK1a−K2bK1K2DK1a+K2bK1+K2In a first order reaction A → B, if k is rate constant and initial concentration of the reactant A is 2 M then the half life of the reaction is:
Alog2kBlog2k√0.5Cln2kD0.6930.5k
In a chemical reaction , A+2BK⇐⇒2c+D, the initial concentration of B was 1.5 times of the concentrations of A , but the equilibrium concentrations of A and B were found to be equal . The equilibrium constant (K) for the aforesaid chemical reaction is :
View SolutionIn a chemical reaction , A+2BK⇐⇒2c+D, the initial concentration of B was 1.5 times of the concentrations of A , but the equilibrium concentrations of A and B were found to be equal . The equilibrium constant (K) for the aforesaid chemical reaction is :
View SolutionFor an elementary chemical reaction, A2k1⇐===⇒k−12A, the expression for d[A]dt is
View SolutionFor an elementary chemical reaction, A2k1⇐===⇒k−12A, the expression for d[A]dt is
View Solution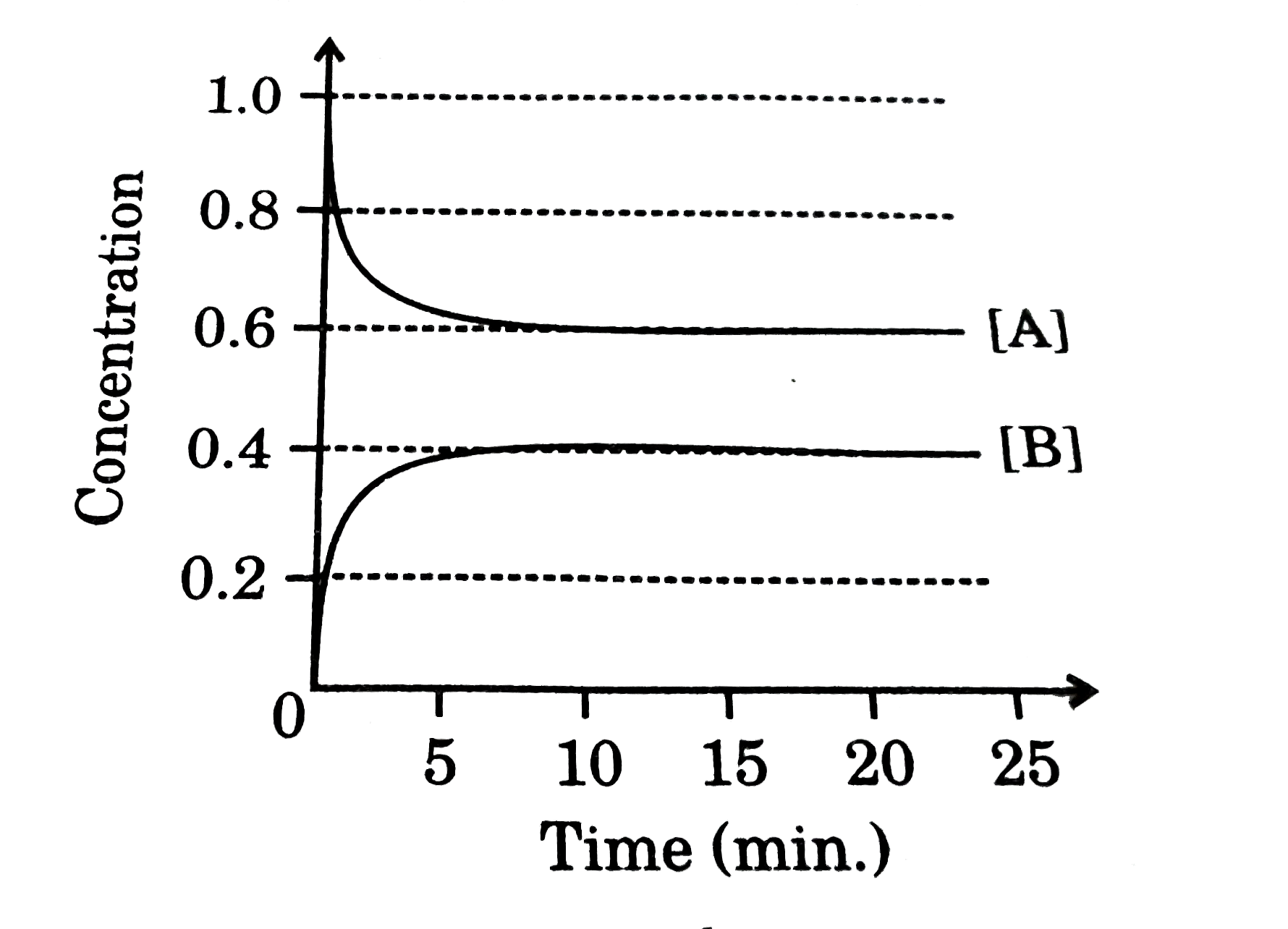
For the reversible reaction Akf⇐===⇒kbB (having Ist order in both direction) the concentration as a function of time are given for a certain experimantal run.
At what time (t) is the rete of change of concentration A equal to the rate of change of concentration of B in magnitude?
View Solution
