The quantity of .14C as well as that of .14CO2 present in the atmosphere remains constant. The concentration of .14C in all living organisms remains almost constant during their life time. After their death, .14C is not taken up by them but the content of .14C assimilated begins to decay by emitting β− particles, with half-life period of 5568 years. The decay rate at the time of death of plant is 16.1counts per minute per gram of carbon. Hence, by measuring the decay rate of the dead matter, the age of matter can be calculated , e.g. if decay rate of sample of wood is found to be N distengrations per minute per gram of carbon after t years, then N=N0e−λt
where λ= disntegration constant and
N0= number of disntegrations per minute per gram when the plant had just died.
.14C is
an artificial radioactive isotope
a natural radioactive isotope
a natural non-radioactive isotope
an artifical non-radioactive isotope
The correct Answer is:A
Topper's Solved these Questions
- CHEMICAL KINETICS AND RADIOACTIVITYBOOK - FIITJEECHAPTER - CHEMICAL KINETICS AND RADIOACTIVITYEXERCISE - Assignment problems (Objective) Level-II (Comprehension-IV)
2 Videos
- CHEMICAL KINETICS AND RADIOACTIVITYBOOK - FIITJEECHAPTER - CHEMICAL KINETICS AND RADIOACTIVITYEXERCISE - Assignment problems (Objective) Level-II (Comprehension-V)
5 Videos
- CHEMICAL KINETICS AND RADIOACTIVITYBOOK - FIITJEECHAPTER - CHEMICAL KINETICS AND RADIOACTIVITYEXERCISE - Assignment problems (Objective) Level-II ( Comprehension-II)
3 Videos
- CHEMICAL EQUILIBRIUMBOOK - FIITJEECHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - MATCHING TYPE QUESTIONS
3 Videos
- CHEMISTRY IN EVERY DAY LIFE BOOK - FIITJEECHAPTER - CHEMISTRY IN EVERY DAY LIFE EXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE) Level - II (Numerical Based Questions)
5 Videos
Similar Questions
A collision between high energy molecules overcomes the forces of repulsion and brings the formation of an unstable molecule cluster, called activated complex. The life span of an activatd complex is very small. Thus, the activated complex breaks either into reactants again or new substances, i.e. products. The activation energy (Ea) depends upon the nature of chemical bonds undergoing rupture and is independent of enthalpies of reactants and products. The energy changes during exothermic and endothermic versus the progress of the reaction are as shown below :
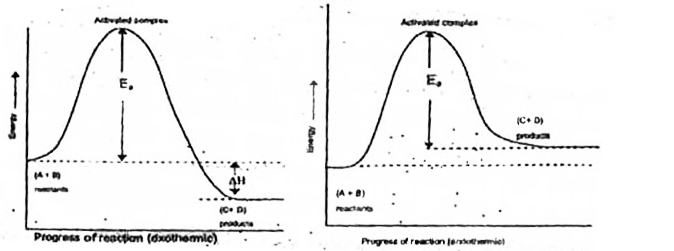
When temperature is increased, the number of active molecule increases, i.e. the number of effective collisions will increase and the rate of reaction will increase.
Activation energy (Ea)=E(activated complex)−E(ground state)
ΔH=Ea(f)−Ea(b)
The activation energy of exothermic reaction , A→B, is 80kJ. The heat of reaction is 200kJ. The activation energy for the reaction, B→A, will be
View SolutionWhen the temperature is increased, heat is supplied which increases the kinetic energy of the reacting molecules. This shall increase the number of collisions and ultimately the rate of reaction shall be enhanced. Arrhenius suggested a equation which describes K as a function of temperature, i.e.
k=Ae−Ea/RT
where
k= rate constant
A= a constant (frequency factor)
Ea= energy of activation
log10k=log10A−Ea2.303R[1R]
Y=C+MX
It is the equation of straight line with negative slope. On plotting log10k against [1T] we get a straight line as shown below :
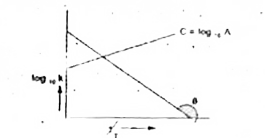
The slope gives activation energy and intercept gives frequency factor.
Also log.k2k1=Ea2.303[T2−T1T1T2]
The rate constant of a reaction is increased by 5% when its temperature is raised from 27∘C to 28∘C . The activation energy of the reaction in kJ/mol is
View SolutionIf a unimolecular reaction, A(g)→ Products, takes place according to the mechanism
(I)A+Ak1⇐===⇒k−1Aa+A
(II)Aa−−→k2P
where k1, k−1 and k2 are the rate constants and P,A and Aa stand for product molecule, normal molecule of reactant and activated molecules of reactant and activated molecules of reactant respectively.
Which of the following expressions are correct?
View Solution

Which of the following combination is correct ?
View SolutionHow many of the following are water soluble vitamins ?
A, B, C, D , K, E
View SolutionA bone containing 200 g carbon-14 has beta -decay rate of 375 decay/min. Calculate the time that has elapsed since the death of the living one. Given the rate of decay for the living organism is equal to 15 decay per min per gram of carbon and half-life of carbon-14 is 5730 years.
View SolutionCarbon -14 used to determine the age of organic material. The procedure is absed on the formation of C^(14) by neutron capture iin the upper atmosphere. ._(7)N^(14)+._(0)n^(1) rarr ._(6)C^(14)+._(1)H^(1) C^(14) is absorbed by living organisms during photosynthesis. The C^(14) content is constant in living organism. Once the plant or animal dies, the uptake of carbon dioxide by it ceases and the level of C^(14) in the dead being falls due to the decay, which C^(14) undergoes. ._(6)C^(14)rarr ._(7)N^(14)+beta^(c-) The half - life period of C^(14) is 5770 year. The decay constant (lambda) can be calculated by using the following formuls : lambda=(0.693)/(t_(1//2)) The comparison of the beta^(c-) activity of the dead matter with that of the carbon still in circulation enables measurement of the period of the isolation of the material from the living cycle. The method, however, ceases to be accurate over periods longer than 30000 years. The proportion of C^(14) to C^(12) in living matter is 1:10^(12) . A nuclear explosion has taken place leading to an increase in the concentration of C^(14) in nearby areas. C^(14) concentration is C_(1) in nearby areas and C_(2) in areas far away. If the age of the fossil is determined to be T_(1) and T_(2) at the places , respectively, then
View SolutionThe half-life of .6C14 is 5730 years. What fraction of a sample of .6C14 will remain unchanged after a period of five half-llves ?
View SolutionThe half-life for decay of .14C by β−emission is 5730 years. The fraction of .14C decays, in a sample that is 22,920 years old, would be
View SolutionThe half life of 6C14, if decay constant 6.31×10−4 is
View SolutionThe half-life of C^(14) is 5760 years . For a 200 mg sample of C^(14) , the time taken to change to 25 mg is -
View Solution14C के रेडियोऐक्टिव क्षय की अर्द्ध आयु 5730 वर्ष है। क्षय या विघटन स्थिरांक की गणना कीजिए।
View SolutionThe quantity of .^(14)C as well as that of .^(14)CO_(2) present in the atmosphere remains constant. The concentration of .^(14)C in all living organisms remains almost constant during their life time. After their death, .^(14)C is not taken up by them but the content of .^(14)C assimilated begins to decay by emitting beta- particles, with half-life period of 5568 years. The decay rate at the time of death of plant is 16.1 counts per minute per gram of carbon. Hence, by measuring the decay rate of the dead matter, the age of matter can be calculated , e.g. if decay rate of sample of wood is found to be N distengrations per minute per gram of carbon after t years, then N=N_(0)e^(-lambda t) where lambda= disntegration constant and N_(0)= number of disntegrations per minute per gram when the plant had just died. .^(14)C is present in environmental because of
View SolutionThe quantity of .^(14)C as well as that of .^(14)CO_(2) present in the atmosphere remains constant. The concentration of .^(14)C in all living organisms remains almost constant during their life time. After their death, .^(14)C is not taken up by them but the content of .^(14)C assimilated begins to decay by emitting beta- particles, with half-life period of 5568 years. The decay rate at the time of death of plant is 16.1 counts per minute per gram of carbon. Hence, by measuring the decay rate of the dead matter, the age of matter can be calculated , e.g. if decay rate of sample of wood is found to be N distengrations per minute per gram of carbon after t years, then N=N_(0)e^(-lambda t) where lambda= disntegration constant and N_(0)= number of disntegrations per minute per gram when the plant had just died. In a dead plant, the decay rate will be
View SolutionThe quantity of .14C as well as that of .14CO2 present in the atmosphere remains constant. The concentration of .14C in all living organisms remains almost constant during their life time. After their death, .14C is not taken up by them but the content of .14C assimilated begins to decay by emitting β− particles, with half-life period of 5568 years. The decay rate at the time of death of plant is 16.1counts per minute per gram of carbon. Hence, by measuring the decay rate of the dead matter, the age of matter can be calculated , e.g. if decay rate of sample of wood is found to be N distengrations per minute per gram of carbon after t years, then N=N0e−λt
where λ= disntegration constant and
N0= number of disntegrations per minute per gram when the plant had just died.
The basis for carbon - 14 dating method is that the
View Solution
