When the temperature is increased, heat is supplied which increases the kinetic energy of the reacting molecules. This shall increase the number of collisions and ultimately the rate of reaction shall be enhanced. Arrhenius suggested a equation which describes K as a function of temperature, i.e.
k=Ae−Ea/RT
where
k= rate constant
A= a constant (frequency factor)
Ea= energy of activation
log10k=log10A−Ea2.303R[1R]
Y=C+MX
It is the equation of straight line with negative slope. On plotting log10k against [1T] we get a straight line as shown below :
![When the temperature is increased, heat is supplied which increases the kinetic energy of the reacting molecules. This shall increase the number of collisions and ultimately the rate of reaction shall be enhanced. Arrhenius suggested a equation which describes K as a function of temperature, i.e. k=Ae^(-E(a)//RT) where k= rate constant A= a constant (frequency factor) E(a)= energy of activation log(10)k=log(10)A-(E(a))/(2.303R)[(1)/(R )] Y=C+MX It is the equation of straight line with negative slope. On plotting log(10)k against [(1)/(T)] we get a straight line as shown below : The slope gives activation energy and intercept gives frequency factor. Also log.(k(2))/(k(1))=(E(a))/(2.303)[(T(2)-T(1))/(T(1)T(2))] The activation energy of a reaction is 9 kcal/mol. The increase in rate constant when its temperature is raised from 295 to 300K is approximately](https://d10lpgp6xz60nq.cloudfront.net/physics_images/FIITJEE_CHE_MB_02_C02_E05_092_Q01.png)
The slope gives activation energy and intercept gives frequency factor.
Also log.k2k1=Ea2.303[T2−T1T1T2]
The activation energy of a reaction is 9 kcal/mol. The increase in rate constant when its temperature is raised from 295 to 300K is approximately
10%
50%
100%
255%
The correct Answer is:D
Topper's Solved these Questions
- CHEMICAL KINETICS AND RADIOACTIVITYBook:FIITJEEChapter:CHEMICAL KINETICS AND RADIOACTIVITYExercise:Matching list type question
Explore 3 Videos
- CHEMICAL KINETICS AND RADIOACTIVITYBook:FIITJEEChapter:CHEMICAL KINETICS AND RADIOACTIVITYExercise:Matching type single correct
Explore 3 Videos
- CHEMICAL KINETICS AND RADIOACTIVITYBook:FIITJEEChapter:CHEMICAL KINETICS AND RADIOACTIVITYExercise:Assignment problems (Objective) Level-II (Comprehension-IV)
Explore 2 Videos
- CHEMICAL EQUILIBRIUMBook:FIITJEEChapter:CHEMICAL EQUILIBRIUMExercise:MATCHING TYPE QUESTIONS
Explore 3 Videos
- CHEMISTRY IN EVERY DAY LIFE Book:FIITJEEChapter:CHEMISTRY IN EVERY DAY LIFE Exercise:ASSIGNMENT PROBLEMS (OBJECTIVE) Level - II (Numerical Based Questions)
Explore 5 Videos
Similar Questions

View Solution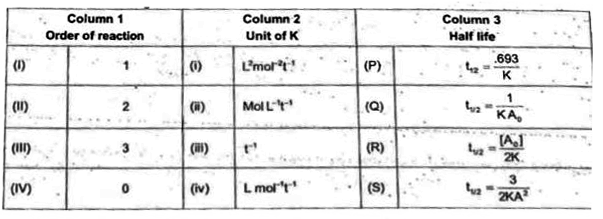
View SolutionA collision between high energy molecules overcomes the forces of repulsion and brings the formation of an unstable molecule cluster, called activated complex. The life span of an activatd complex is very small. Thus, the activated complex breaks either into reactants again or new substances, i.e. products. The activation energy (Ea) depends upon the nature of chemical bonds undergoing rupture and is independent of enthalpies of reactants and products. The energy changes during exothermic and endothermic versus the progress of the reaction are as shown below :
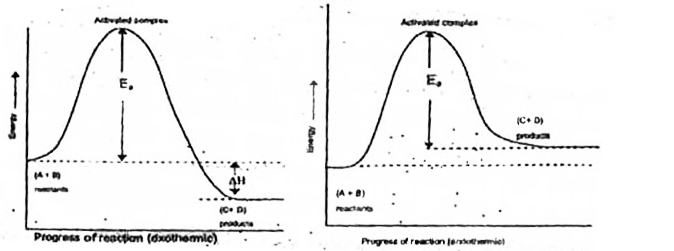
When temperature is increased, the number of active molecule increases, i.e. the number of effective collisions will increase and the rate of reaction will increase.
Activation energy (Ea)=E(activated complex)−E(ground state)
ΔH=Ea(f)−Ea(b)
The activation energy of exothermic reaction , A→B, is 80kJ. The heat of reaction is 200kJ. The activation energy for the reaction, B→A, will be
View Solution

Which of the following combination is correct ?
View SolutionHow many of the following are water soluble vitamins ?
A, B, C, D , K, E
View SolutionThe rate of reaction increases isgnificantly with increase in temperature. Generally, rate of reactions are doubled for every 10^(@)C rise in temperature. Temperature coefficient gives us an idea about the change in the rate of a reaction for every 10^(@)C change in temperature. "Temperature coefficient" (mu) = ("Rate constant of" (T + 10)^(@)C)/("Rate constant at" T^(@)C) Arrhenius gave an equation which describes aret constant k as a function of temperature k = Ae^(-E_(a)//RT) where k is the rate constant, A is the frequency factor or pre-exponential factor, E_(a) is the activation energy, T is the temperature in kelvin, R is the universal gas constant. Equation when expressed in logarithmic form becomes log k = log A - (E_(a))/(2.303 RT) For a reaction E_(a) = 0 and k = 3.2 xx 10^(8)s^(-1) at 325 K . The value of k at 335 K would be
View SolutionThe rate of reaction increases isgnificantly with increase in temperature. Generally, rate of reactions are doubled for every 10∘C rise in temperature. Temperature coefficient gives us an idea about the change in the rate of a reaction for every 10∘C change in temperature.
Temperature coefficient(μ)=Rate constant of(T+10)∘CRate constant atT∘C
Arrhenius gave an equation which describes aret constant k as a function of temperature
k=Ae−Ea/RT
where k is the rate constant, A is the frequency factor or pre-exponential factor, Ea is the activation energy, T is the temperature in kelvin, R is the universal gas constant.
Equation when expressed in logarithmic form becomes
logk=logA−Ea2.303RT
For which of the following reactions k310/k300 would be maximum?
View SolutionThe rate of reaction increases isgnificantly with increase in temperature. Generally, rate of reactions are doubled for every 10∘C rise in temperature. Temperature coefficient gives us an idea about the change in the rate of a reaction for every 10∘C change in temperature.
Temperature coefficient(μ)=Rate constant of(T+10)∘CRate constant atT∘C
Arrhenius gave an equation which describes aret constant k as a function of temperature
k=Ae−Ea/RT
where k is the rate constant, A is the frequency factor or pre-exponential factor, Ea is the activation energy, T is the temperature in kelvin, R is the universal gas constant.
Equation when expressed in logarithmic form becomes
logk=logA−Ea2.303RT
Activation energies of two reaction are Ea and Ea' with Ea>E'a. If the temperature of the reacting systems is increased form T1 to T2 (k' is rate constant at higher temperature).
View SolutionThe rate of reaction increases isgnificantly with increase in temperature. Generally, rate of reactions are doubled for every 10∘C rise in temperature. Temperature coefficient gives us an idea about the change in the rate of a reaction for every 10∘C change in temperature.
Temperature coefficient(μ)=Rate constant of(T+10)∘CRate constant atT∘C
Arrhenius gave an equation which describes aret constant k as a function of temperature
k=Ae−Ea/RT
where k is the rate constant, A is the frequency factor or pre-exponential factor, Ea is the activation energy, T is the temperature in kelvin, R is the universal gas constant.
Equation when expressed in logarithmic form becomes
logk=logA−Ea2.303RT
For the given reactions, following data is given
P→Qk1=1015exp(−2000T)C→Dk2=1014exp(−1000T)
Temperature at which k1=k2 is
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy E_(a) Large the value of activation energy, smaller the value of rate constant k . Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k . E_(f) = Activation energy of forward reaction E_(b) = Activation energy of backward reaction Delta H = E_(f) - E_(b) E_(f) = threshold energy The rate constant of a certain reaction is given by k = Ae^(-E_(a)//RT) (where A = Arrhenius constant). Which factor should be lowered so that the rate of reaction may increase?
View SolutionThe rate constant of most of the reaction increases with increase in temperature. According to the Arrhenius equation, k = Ae^(-E_(a)//RT) . The curve of rate constant 'k' against temperature 'T' will be.
View SolutionThe rate of chemical reaction are strongly affected by temperature . Arrhenius (1889) gave following relation between rate contant and temperature . k=Ae^(-E_(a)//RT)" ".....(i) This equation is called Arrhenius equation. The constant 'A' is caleld Arrhenius of pre-exponential factor. Logarithm of equation (i) given : log_(10)k=log_(10)A(E_(a))/(2.3030RT)" ".....(ii) The rate constant for a reaction is . log_(10)"sec"^(-1)=14-(1.25xx10^(4)K)/(T) " ".....(iii) The pre-exponential factor or frequency factor of the reaction under consideration is :
View SolutionThe rate of chemical reaction are strongly affected by temperature . Arrhenius (1889) gave following relation between rate contant and temperature .
k=Ae−Ea/RT .....(i)
This equation is called Arrhenius equation. The constant 'A' is caleld Arrhenius of pre-exponential factor. Logarithm of equation (i) given :
log10k=log10AEa2.3030RT .....(ii)
The rate constant for a reaction is .
log10sec−1=14−1.25×104KT .....(iii)
At what temperature, rate constant of the reaction is equal to the pre-exponenntial factor ?
View SolutionThe rate of chemical reaction are strongly affected by temperature . Arrhenius (1889) gave following relation between rate contant and temperature . k=Ae^(-E_(a)//RT)" ".....(i) This equation is called Arrhenius equation. The constant 'A' is caleld Arrhenius of pre-exponential factor. Logarithm of equation (i) given : log_(10)k=log_(10)A(E_(a))/(2.3030RT)" ".....(ii) The rate constant for a reaction is . log_(10)"sec"^(-1)=14-(1.25xx10^(4)K)/(T) " ".....(iii) Energy of activation in K cal "mol"^(-1) is:
View SolutionWhen the temperature is increased, heat is supplied which increases the kinetic energy of the reacting molecules. This shall increase the number of collisions and ultimately the rate of reaction shall be enhanced. Arrhenius suggested a equation which describes K as a function of temperature, i.e.
k=Ae−Ea/RT
where
k= rate constant
A= a constant (frequency factor)
Ea= energy of activation
log10k=log10A−Ea2.303R[1R]
Y=C+MX
It is the equation of straight line with negative slope. On plotting log10k against [1T] we get a straight line as shown below :
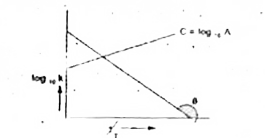
The slope gives activation energy and intercept gives frequency factor.
Also log.k2k1=Ea2.303[T2−T1T1T2]
The rate constant of a reaction is increased by 5% when its temperature is raised from 27∘C to 28∘C . The activation energy of the reaction in kJ/mol is
View Solution
