In which of the following geometrical isomerism is possible ?
All of these
The correct Answer is:2
To determine which of the given compounds can exhibit geometrical isomerism (GI), we need to follow these steps:
Step 1: Understand the Conditions for Geometrical Isomerism
Geometrical isomerism occurs under two main conditions:
1. There must be restricted rotation around a bond (usually a double bond).
2. The substituents attached to the atoms involved in the double bond must be different.
Step 2: Analyze the First Compound
- The first compound has a double bond and two methyl groups attached to one of the carbon atoms.
- Since both substituents on this carbon are the same (methyl groups), there is no possibility for geometrical isomerism.
- Conclusion: GI is not possible for the first compound.
Step 3: Analyze the Second Compound
- The second compound contains a double bond between two nitrogen atoms, with one nitrogen having a lone pair and a phenyl group attached.
- The other nitrogen also has a phenyl group attached.
- Here, we have different substituents (lone pair and phenyl group) on one nitrogen, which allows for the formation of geometrical isomers (cis and trans forms).
- Conclusion: GI is possible for the second compound.
Step 4: Analyze the Third Compound
- The third compound has a double bond, but both substituents on one of the carbon atoms are hydrogen atoms.
- Since both substituents are the same, there is no possibility for geometrical isomerism.
- Conclusion: GI is not possible for the third compound.
Final Conclusion
Among the three compounds analyzed, only the second compound shows geometrical isomerism.
Summary of the Answer
- Only the second compound shows geometrical isomerism.
---
Geometrical isomerism occurs under two main conditions:
1. There must be restricted rotation around a bond (usually a double bond).
2. The substituents attached to the atoms involved in the double bond must be different.
- The first compound has a double bond and two methyl groups attached to one of the carbon atoms.
- Since both substituents on this carbon are the same (methyl groups), there is no possibility for geometrical isomerism.
- Conclusion: GI is not possible for the first compound.
- The second compound contains a double bond between two nitrogen atoms, with one nitrogen having a lone pair and a phenyl group attached.
- The other nitrogen also has a phenyl group attached.
- Here, we have different substituents (lone pair and phenyl group) on one nitrogen, which allows for the formation of geometrical isomers (cis and trans forms).
- Conclusion: GI is possible for the second compound.
- The third compound has a double bond, but both substituents on one of the carbon atoms are hydrogen atoms.
- Since both substituents are the same, there is no possibility for geometrical isomerism.
- Conclusion: GI is not possible for the third compound.
Among the three compounds analyzed, only the second compound shows geometrical isomerism.
- Only the second compound shows geometrical isomerism.
Topper's Solved these Questions
- HYDROCARBONSBook:AAKASH INSTITUTEChapter:HYDROCARBONSExercise:Assignment(Section - A) (Obejctive type question)
Explore 55 Videos
- HYDROCARBONSBook:AAKASH INSTITUTEChapter:HYDROCARBONSExercise:Assignment(Section - B) (Obejctive type question)
Explore 13 Videos
- HYDROCARBONSBook:AAKASH INSTITUTEChapter:HYDROCARBONSExercise:TRY YOURSELF
Explore 78 Videos
- HALOALKANES AND HALOARENES Book:AAKASH INSTITUTEChapter:HALOALKANES AND HALOARENES Exercise:ASSIGNMENT SECTION -D
Explore 15 Videos
- HYDROGENBook:AAKASH INSTITUTEChapter:HYDROGENExercise:ASSIGNMENT (SECTION - D) (Assertion-Reason Type question)
Explore 15 Videos
Similar Questions
Knowledge Check
Geometrical isomerism is possible in
AAcetone-oxineBIsobuteneCAcetophenone-oximeDBenzophenone-oximeGeometrical isomerism is possible in :
Aformaldehyde hydrozoneBacetone oximeCacetophebnone oximeDbenzophenone oximeGeometrical isomerism is possible in :
A B
B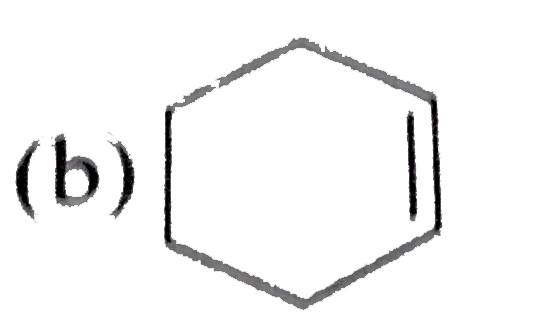 C
C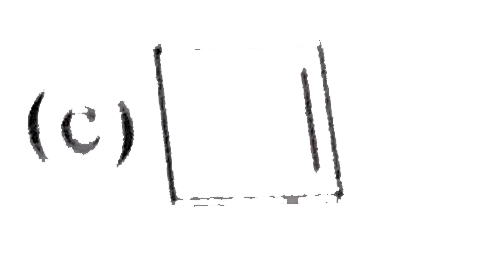 D
D
Which of the following shows geometrical isomerism
View SolutionWhich of the following show geometrical isomerism?
View SolutionGeometrical isomerism is possible in case of
View SolutionWhich of the following shows geometrical isomerism?
View SolutionWhich of the following shows geometrical isomerism.
View Solution