Show that the wor done by a force is equal to change in potential energy .

Video Solution

Text Solution

Generated By DoubtnutGPT

To show that the work done by a force is equal to the change in potential energy, we will follow these steps:
Step 1: Understand the Concept of Work Done
Work done (W) by a force is defined as the force (F) applied on an object multiplied by the displacement (s) in the direction of the force. Mathematically, it is given by:
$W = F \cdot s$
When the force is acting against gravity, we will consider the gravitational force acting on an object of mass $m$ .
Step 2: Define Potential Energy
Potential energy (PE) is the energy possessed by an object due to its position in a gravitational field. The potential energy at a height $h$ is given by:
$P E = m g h$
where $g$ is the acceleration due to gravity.
Step 3: Consider Two Heights
Let’s consider an object that is raised from an initial height $h_{1}$ to a final height $h_{2}$ . The potential energy at these heights can be expressed as:
- Initial potential energy at height $h_{1}$ :
$P E_{1} = m g h_{1}$
- Final potential energy at height $h_{2}$ :
$P E_{2} = m g h_{2}$
Step 4: Calculate the Change in Potential Energy
The change in potential energy ( $Δ P E$ ) when the object is moved from height $h_{1}$ to height $h_{2}$ is given by:
$Δ P E = P E_{2} - P E_{1} = m g h_{2} - m g h_{1}$
Step 5: Relate Work Done to Change in Potential Energy
When the object is lifted, the work done against the gravitational force is equal to the change in potential energy. The work done (W) in lifting the object to height $h_{2}$ is:
$W = m g h_{2} - m g h_{1} = Δ P E$
Conclusion
Thus, we have shown that the work done by a force in lifting an object is equal to the change in potential energy:
$W = Δ P E$

Updated on:18/9/2024

Separation between the plates of a parallel plate capacitor, connected to a battery (zero resistance) of constant emf. is increased with constant (very slow) speed by external forces. During the process, W is the work done by external forces, $Δ U$ is the change in potential energy of the capacitor, $W_{b}$ is the work done by the battery and H is the heat loss in the circuit. Then
A $W + W_{b} = Δ U$
B $H \neq 0$
C $H = Δ U$
D $W = 0$
Asseration : Displacement time graph of a particle moving in a straight line is shown in figure. Work done by all the forces between time interval $t_{1}$ and $t_{2}$ is definitely zero.
,
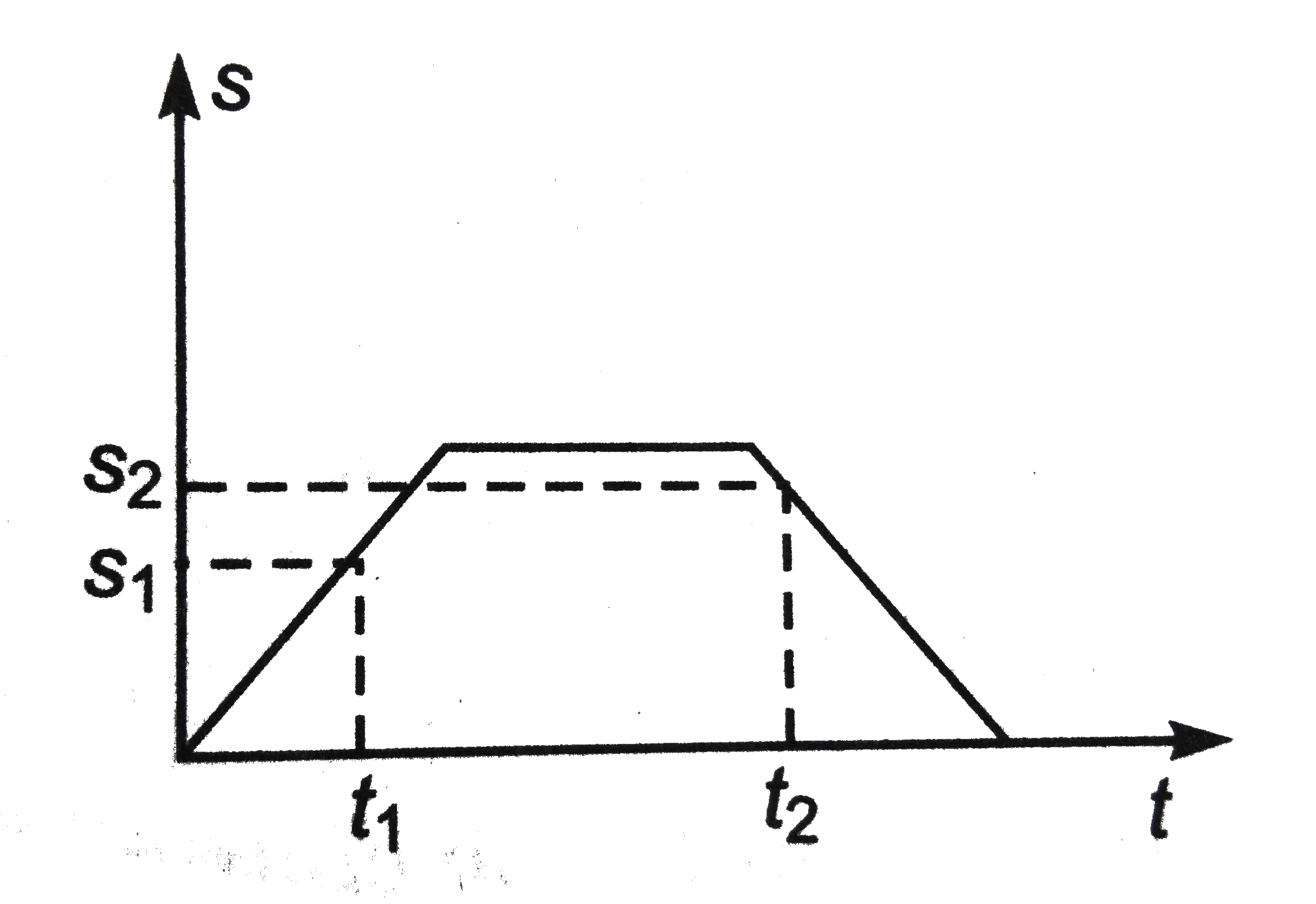Reason : Work done by all the forces is equal to change in kinetic energy.
AIf both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
BIf both Assertion and Reason are true and the Reason is not the correct explanation of the Assertion.
CIf Assertion is true, but the Reason is false
DIf Assertion is false but the Reason is true.
The total work done on a particle is equal to the change in its mechanical energy
Aif the forces acting on are conservative
Bif gravitational force alone acts on it
Cif elastic alone acts on it.
Dnone of these