A mass m is placed at P a distance h along the normal through the centre O of a thin circular ring of mass M and radius r Fig.
If the mass is removed futher away such that OP becomes 2h, by what factor the force of gravitational will decrease, if h=r ?
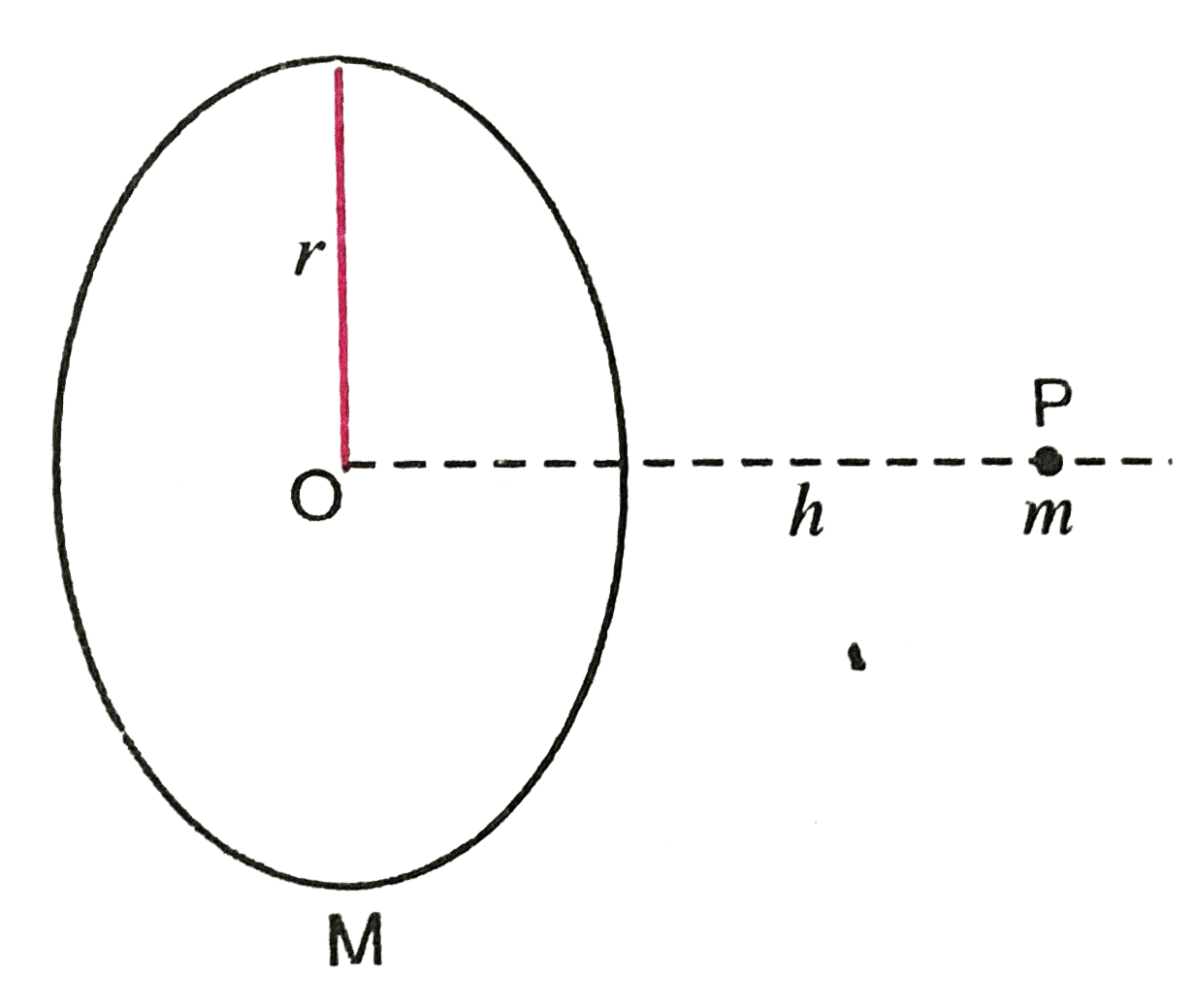
Gravitational force on the object at point P is
F=GMmh(r2+h2)32
when h = r
F=GMmr(r2+r2)32=GMm2√2r2
When h becomes 2h
F.=GMm2h(r2+4h2)32
When h = r
And F.=2GMmr(r2+4r2)32=2GMm5√5r2
∴F.F=4√25√5
or F.=4√25√5F
Topper's Solved these Questions
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Higher Order Thinking Skills & Advanced Level
15 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Revision Exercises (very short answer questions)
30 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - NCERT FILE (Additional Exercises)
4 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
Similar Questions
Knowledge Check
The escape velocity form the centre of a unifrom ring of mass M and radius R is :
A√2GMRB√GMRC√GM2RD√GMRFor a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMRA point mass m0 is placed at distance R/3 from the centre of spherical shell of mass m and radius R. the gravitational force on the point mass m0 is
A4Gmm0R2BzeroC9Gmm0R2DNone of these
Calculate gravitational field intensity at a distance x on the axis from centre of a uniform disc of mass M and radius R .
View SolutionThe M.I. of a thin ring of mass M and radius R about an axis through the diameter in its plane will be:
View SolutionA particle of mass m is ocated at a distance r from the centre of shell of mass M and radius R. The force between the shell and mass F(r). The plot of F(r) ve r is :
View SolutionA particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane.
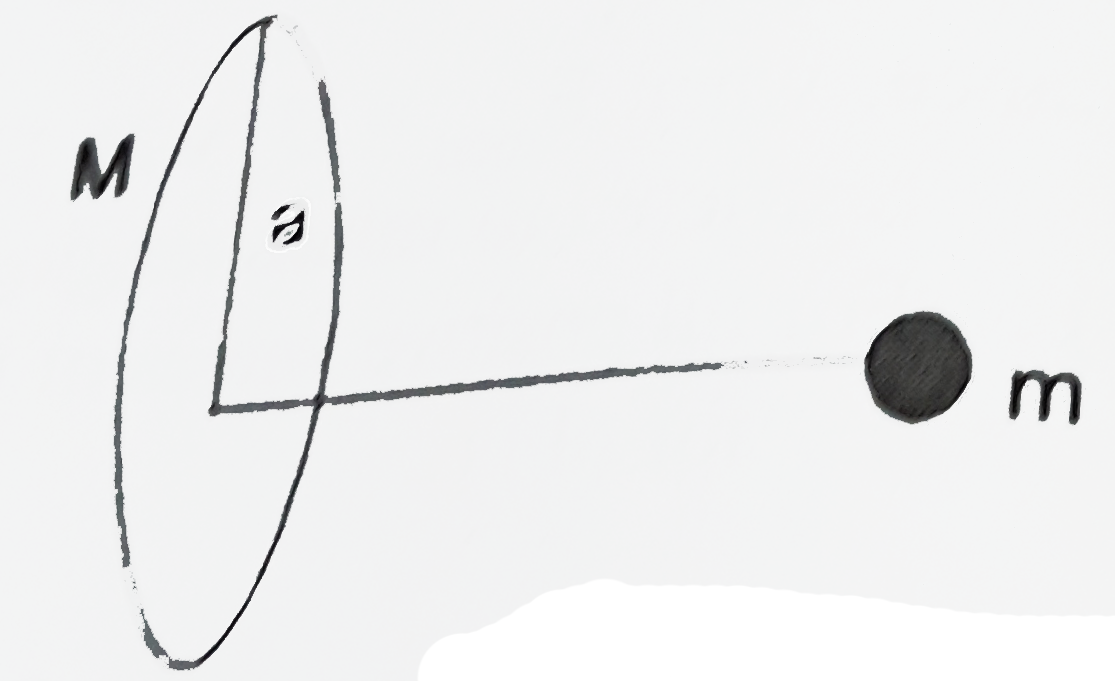
if x<<a, the particle of mass m will:
View SolutionA particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane.
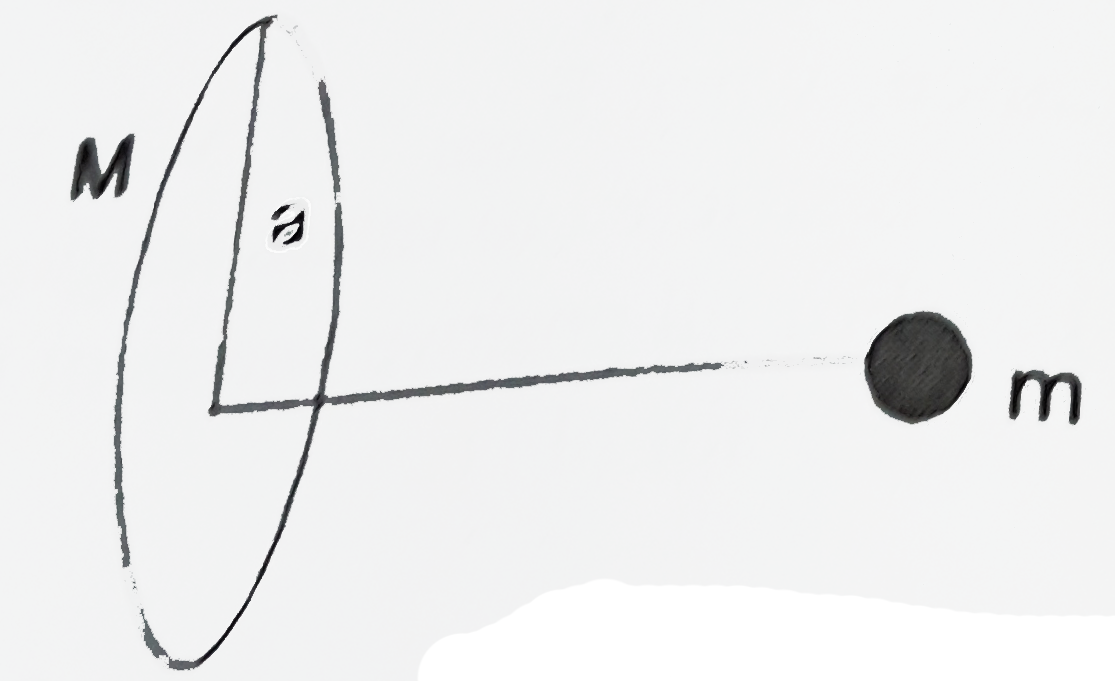
Gravitational potential energy of this system.
View Solution
